Die hier gegebene andere Antwort von 55,1 cm gilt für eine gerade Pyramide, also wenn die Spitze senkrecht über dem Mittelpunkt des Rechtecks liegt.
Eine Pyramide kann auch schief sein. Dann liegt die Spitze zwar immer noch 8 cm vertikale Distanz über der Grundfläche, aber irgendwo, und die vier Seitenkanten von den Ecken der Grundfläche zur Spitze sind nicht alle gleich lang. Wenn der Mittelpunkt der Grundfläche die Koordinaten (0 | 0 | 0) hat (und die vier Ecken die Koordinaten (-2 | -3 | 0), (2 | -3 | 0), (2 | 3 | 0) und (-2 | 3 | 0)), dann wird die Formel vom Mathecoach
2·4 + 2·6 + 4·√((4/2)2 + (6/2)2 + 82)
für eine Spitze mit den Koordinaten (x | y | 8) zu
2·4 + 2·6
+ √((x+2)2 + (y+3)2 + 82)
+ √((x-2)2 + (y+3)2 + 82)
+ √((x-2)2 + (y-3)2 + 82)
+ √((x+2)2 + (y-3)2 + 82)
und man kann zeigen, dass das Minimum der Drahtlänge bei den Koordinaten (0 | 0 | 8) der Spitze ist, also da wo die Pyramide nicht mehr schief ist.
Drahtlänge in Abhängigkeit von den Koordinaten der Spitze:
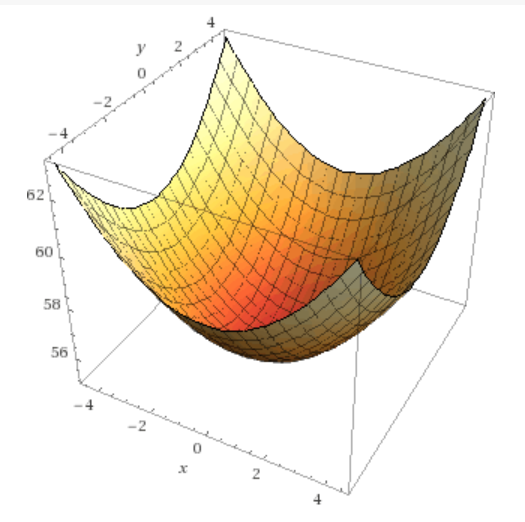
Der Wurzelausdruck ist sowohl beim Mathecoach wie auch bei mir die Formel für die euklidische Distanz zwischen zwei Punkten im dreidimensionalen Raum.