welche Werte kann y annehmen?

Question

Aufgabe:

Welche Werte kann y für eine Funktion 1-y = e^x annehmen?

Problem/Ansatz:

Wie löse ich diese Aufgabe?

Answer 1

y=1-e^x

also y∈ℝ, so dass y≤0

Comments

@rc: Habe etwas Anderes.

Ich weiss aber auch nicht, was mit

Funktion 1-y = e^x

gemeint ist. So definiert man keine Funktion.

Answer 2

Löse die Gleichung nach y auf,

$$1-y = e^x\Rightarrow y=1-e^x$$

Da \(e^x>0\) gilt, sich aber für negative x immer mehr der Null nähert, gilt \(y<1\).

Comments

Ich verstehe leider die Erklärung nicht. Kannst du mir das bitte nochmal erklären

Answer 3

Annahme das Wort "Funktion" in der Fragestellung ist ein Verschreiber.

Ich versuche es ohne LaTeX, damit es (hoffentlich) lesbarer ist.

1-y = e^x      | + y - e^x

1 - e^x = y

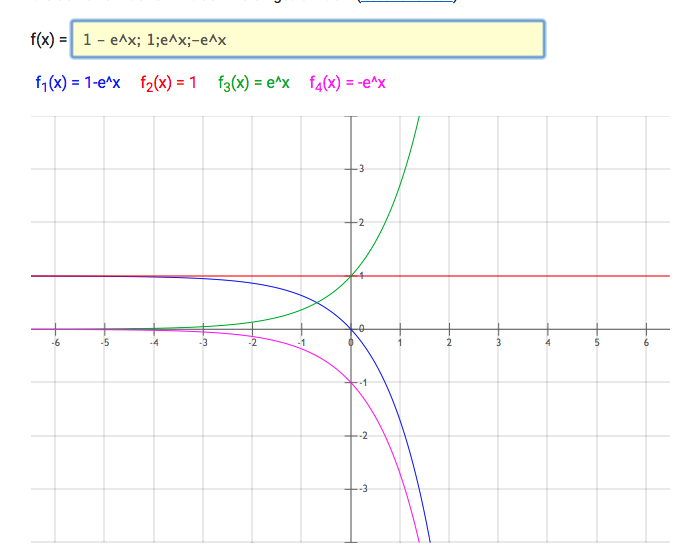
Du weisst, dass f(x) = e^x alle positiven reellen Zahlen als Wertebereich hat.

g(x) = - e^x hat folglich alle negativen reellen Zahlen als Wertebereich

h(x) = y = 1 - e^x hat alle reellen Zahlen, die kleiner als 1 sind, als Wertebereich.

Somit Wertebereich W = { x Element ℝ | x < 1 } . 

Graphisch:

~plot~ 1 - e^x; 1;e^x;-e^x ~plot~

EDIT, da Plot nicht direkt angezeigt wird.: