Wie lang ist die Grundlinie des Dreiecks zu wählen?

Question

Aufgabe:

Einem Halbkreis mit r=6cm ist ein gleichschenkeliges Dreieck von größtem Flächeninhalt einzuschreiben, dessen Spitze im Mittelpunkt des Halbkreises liegt und dessen Grundlinie parallel zum Durchmesser des Halbkreises ist. Wie lang ist die Grundlinie des Dreiecks zu wählen?

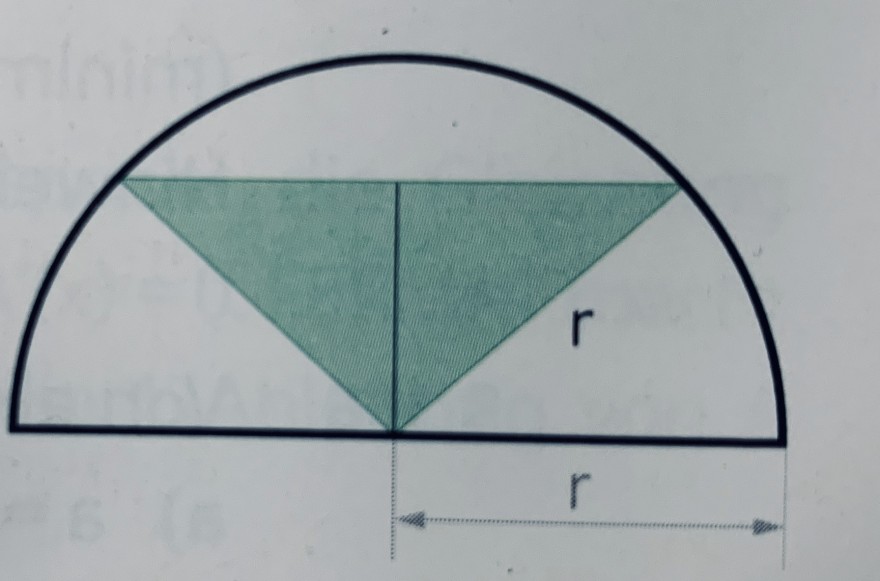
Mein Ansatz war: (c/2)^2=2r^2...

Laut Lösungsheft kommt 6 √2 heraus.

Answer 1

Hallo

 wie kommst du zu deinem Ansatz? in deiner Zeichnung ist die Höhe des Dreiecks gleich c/2, dann würde gelten 2*(c/2)^2=r^2 aber das gilt ja nicht allgemein. (Allerdings hast du zufällig grade das größte Dreieck eingezeichnet)

du musst schon die Fläche  aus A=c*h/2 bestimmen und den Zusammenhang zwischen c und h aus Pythagoras bestimmen und einsetzen, und dann das Max bestimmen

Gruß lul

Comments

Vielen Dank!!!