Kegelförmige Kerze: Warum sehen die beiden Schmelzkurven nicht gleich aus?

Question

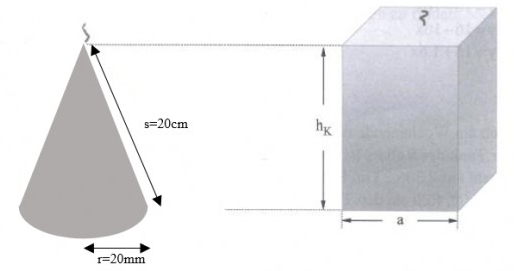
2.1 Eine kegelförmige Kerze wird geschmolzen. Aus dem Wachs soll eine neue Kerze gegossen werden, die die Form einer quadratischen Säule hat und genauso hoch ist wie die kegelförmige Kerze. Hinweis: Rechne mit den gerundeten Werten bei Bedarf weiter.

2.1.1 Berechne das Volumen der kegelförmigen Kerze.

2.1.2 Berechne die Grundseite a der Säulenkerze.

a) Die obenstehende Aufgabe wird der Geometrie zugeordnet. Wozu werden beim Lösen der Aufgabe algebraische Kenntnisse benötigt?

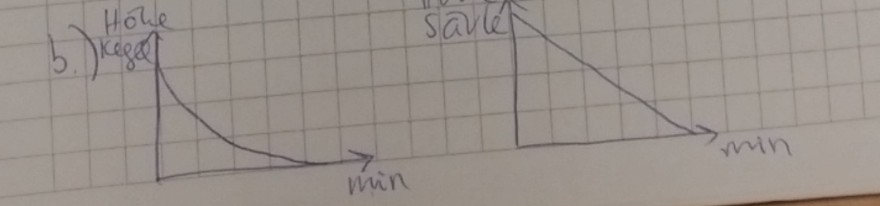
b) Nehmen Sie an, dass beim Abbrennen beider Kerzen gleich viel Wachs pro Minute verbraucht wird. Skizzieren Sie die Abbrennkurven beider Kerzen über den zeitlichen Verlauf. Begründen Sie Ihre Darstellungen in jeweils 2 - 3 Sätzen.

Meine Frage ist, wie die Kurve bei b) aussieht. Also warum sehen die beiden Schmelzkurven nicht gleich aus?

Answer 1

r^2 + h^2 = s^2 --> h = 6·√11 = 19.90 cm

V = 1/3·pi·r^2·h = 8·√11·pi = 83.36 cm³

V = a^2·h --> a = 2·√(pi/3) = 2.047 cm

Stell dir einfach vor welche Zeit für das Abschmelzen bzw. verbrennen einer 1mm hohen Schicht notwendig ist.

Da der Kegel oben eine viel geringere Querschnittsfläche hat geht das abbrennen einer 1 mm hohen Schicht viel schneller als bei der Quaderförmigen Kerze.

Answer 2

Die rechts dargestellte Kerze hat in jeder Höhe den gleichen Querschnitt und brennt daher gleichmäßig bzw. linear ab.

Die kegelförmige Kerze ist oben sehr schmal und brennt zunächst schnell runter, darum verläuft die Kurve am Anfang steil nach unten. Wenn die Kerze dann weiter runtergebrannt ist, wird sie immer breiter und verliert langsamer an Höhe. Der Kurvenverlauf wird dann flacher.