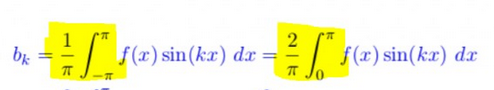Aufgabe:
Berechnen Sie die Fourierreihe der \( 2 \pi \) -periodischen Funktion
$$ f(x)=\left\{\begin{array}{cc} {-1} & {, \text { falls }-\pi<x<0} \\ {0} & {, \text { falls } x \in\{-\pi, 0, \pi\}} \\ {1} & {, \text { falls } 0<x<\pi} \end{array}\right. $$
Lösung:
Die Funktion \( f \) ist ungerade, also sind alle \( a_{k}=0 \) Für die \( b_{k} \) gilt:
$$ \begin{aligned} b_{k} &=\frac{1}{\pi} \int \limits_{-\pi}^{\pi} f(x) \sin (k x) d x=\frac{2}{\pi} \int \limits_{0}^{\pi} f(x) \sin (k x) d x \\ &=\frac{2}{\pi} \int \limits_{0}^{\pi} \sin (k x) d x=-\left.\frac{2}{k \pi} \cos (k x)\right|_{0} ^{\pi} \\ &=-\frac{2}{k \pi}\left((-1)^{k}-1\right) \end{aligned} $$
Problem/Ansatz:Habe es gelb markiert. Ich weiß leider nicht, wie ich auf die Umformung der Integralgrenzen komme und würde mich sehr darüber freuen, wenn mir das jemand erklären könnte. Danke