Die linsenförmige Grundfläche des Schnittkörpers kann man als zweimal den Fläche des Kreissegments bestimmen, und für jenes gibt es eine Formel in Funktion von Kreisradius und Segmenthöhe. Die Segmenthöhe h ist Radius minus halben Mittelpunktabstand d der Kegelgrundflächen, und die Fläche eines Segments ist dann laut Formelsammlung
\( A=r^{2} \cdot \arccos \left(1-\frac{h}{r}\right)-(r-h) \cdot \sqrt{2 r h-h^{2}} \)
Die vertikale Höhe z des Schnittkörpers in Abhängigkeit von Mittelpunktabstand d und Kegelhöhe k notiere ich mal mit
\( z = k (1 - \frac{d}{2r}) \)
Für das Volumen des Schnittkörpers zweier identischer Kegel komme ich so auf
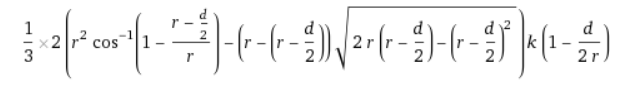
oder vereinfacht
\( \frac{k(d-2 r)\left(d \sqrt{4 r^{2}-d^{2}}-4 r^{2} \operatorname{arccos}\left(\frac{d}{2 r}\right)\right)}{12 r} \)
Falls einer der hier anwesenden Mathematiker meinen Versuch richtig findet, kann man diesen Kommentar gerne zu den Antworten verschieben.