Quadratische Funktion und Gleichung

Question

Hallo,

man muss falls vorhanden die Nullstellen berechnen. Ich brauche vor allem wissen wie man den Funktionsgraphen skizziert.

f: y= -x2+4x-5

Kann mir bitte jemand mit dem helfen?

Vielen Dank Im Voraus

Answer 1

Hallo,

du könntest den Funktionsterm zunächst in die Scheitelpunktform bringen. Dann lässt er sich leichter skizzieren.

(Ergebnis: Scheitelpunkt bei (2|-1), nach unten geöffnete Normalparabel, also keine Nullstellen)

Gruß, Silvia

Answer 2

Hallo,

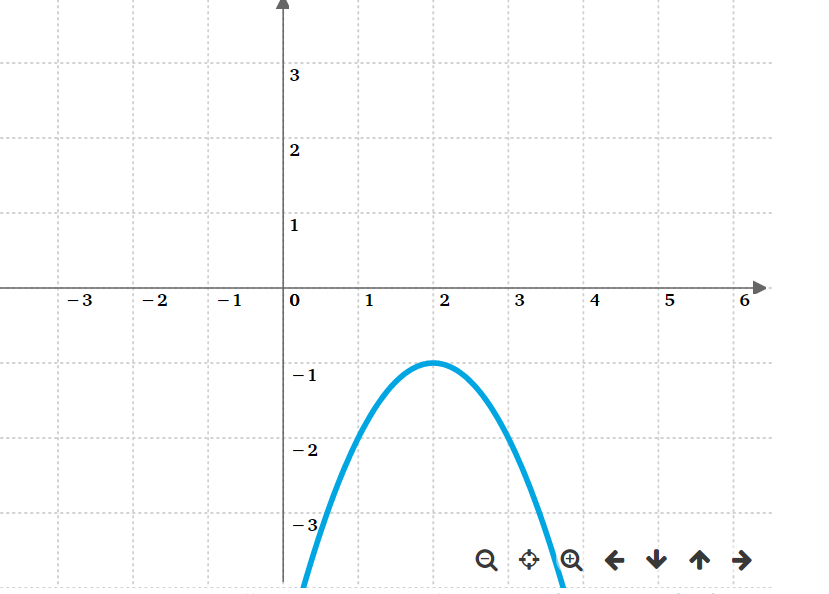
y= -x^2 +4x -5

y=0

0= -x^2 +4x -5 | *(-1)

0= x^2 -4x+5  ->z.b pq. Formel

x_1.2= 2 ± √ (4 -5)

x_1.2= 2 ± √ -1 ->keine Nullstellen

Es gibt 2 komplexe Lösungen , sind aber hier wohl nicht gefragt.

Skizzieren kannst Du die Funktion z.B , indem Du eine Wertetabelle anlegt. Du gibst Dir für x Werte vor .z.B. 1 2 3  -1 -2 -3  usw.

und berechnest durch Einsetzen die y - Werte .

 

Answer 3

Aloha :)

$$y=-x^2+4x-5=-(x^2-4x+5)=-[(x^2-4x+4)+1]=-[(x-2)^2+1]$$$$y=-(x-2)^2-1$$Die Funktion hat keine Nullstellen, weil \(y\) immer \(\le-1\) ist.

~plot~ -x^2+4x-5 ; [[-0,5|4,5|-5|0,5]] ~plot~

Answer 4

In der Regel macht man eine Wertetabelle und verbindet die Punkte dann nur näherungsweise durch eine Parabel.

y= -x^2 + 4x - 5

Oft kann man dann auch schon Y-Achsenabschnitt, Nullstellen und Scheitelpunkt erkennen.