Vektoren als Linearkombination darstellen - Prisma

Question

 hallo :)

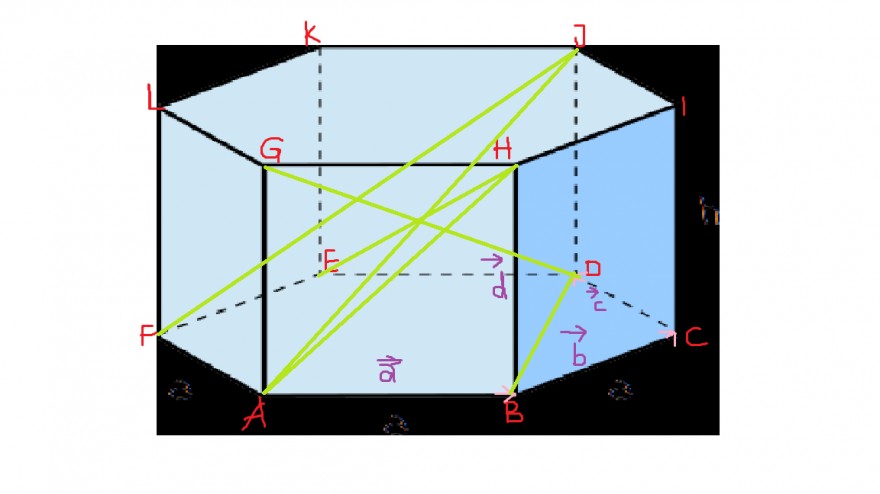
das Bild soll ein Prisma mit regelmäßiger sechseckiger Grundfläche darstellen.

nun muss ich die Vektoren \( \vec{AH} \) \( \vec{AJ} \) \( \vec{EH} \) \( \vec{BD} \) \( \vec{GD} \) und \( \vec{FJ} \)  (grün) als Linearkombinationen aus \( \vec{a} \) \( \vec{b} \) \( \vec{c} \) \( \vec{d} \)  (lila) darstellen.

Leider kann ich Sachen nicht so gut überblicken, wenn es um 3D geht...hab trotzdem versucht, paar Vektoren darzustellen:

AH=d+a

BD=b+c

EH= 1/2 d + a

stimmen die Vektoren? kann mir jmd. auch helfen, die anderen 3 herauszufinden?

Vielen Dank im Voraus 

Comments

Leider kann ich Sachen nicht so gut überblicken, wenn es um 3D geht ...

dann probiere doch mal den Geoknecht3D aus:

klick auf das Bild und rotiere die Szene mit der Maus. Dann bekommst Du einen guten räumlichen Eindruck.

Tipp: \(\vec b = \vec a + \vec c\)

Answer 1

AH=d+a richtig

BD=b+c richtig

EH= 1/2 d + a falsch \( \vec{EH} \) =\( \vec{a} \) -\( \vec{c} \) -\( \vec{b} \) +\( \vec{d} \)

\( \vec{AJ} \) =\( \vec{a} \) +\( \vec{b} \) +\( \vec{c} \) +\( \vec{d} \)

Parallele, gleichlange Vektoren haben den gleichen Namen.

Comments

hallo, wäre GD also b+b+b-d? den Weg, den ich gesucht habe: G->L, dann L->K, dann K->J, dann J->D

---

wäre GD also b+b+b-d?

Nein. \(\vec{GD} = -d + a + b + c = 2b - d\)

G->L, dann L->K, dann K->J, dann J->D

\(\vec{GL} = c, \space \vec{LK} = b , \space \vec{KJ} = a, \space \vec{JD} = -d\). Also $$\begin{aligned}\vec{GL} + \vec{LK} + \vec{KJ} + \vec{JD} &= c + b + a - d \\ &= \underbrace{(c+a)}_{=b} + b - d \\ &= b + b - d \\ &= 2b -d\end{aligned}$$

---

Klick hier - zu Geoknecht3D

Answer 2

Hallo
mach dir klar, dass alle nach oben gehenden Vektoren d sind, und unten  sind auch die je 2 parallelen gleich. dann kannst du es sicher selbst.
z.B. FJ=b+a+d einfach indem du von F nach E mit b  von E nach D  mit a von D nach J mit d gehst.
Gruß lul