Hallo Maluma,
Die erste Division ist einfach. Der Rest ist \(-3x^2+5x - 2\). Die zweite ist schon aufwendiger - man hat Möglichkeiten, sich zu verrechnen ;-). Also ganz ausführlich:
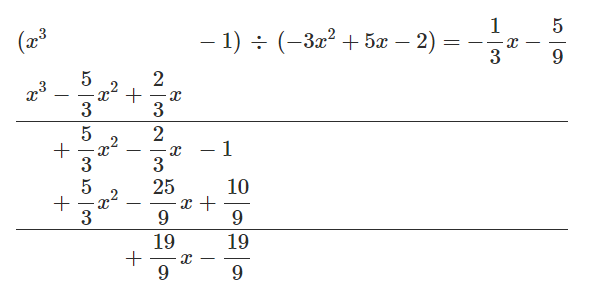
Latex: \begin{alignat*}{1} (x^3 &&&-1) \,\div\, (-3x^2 + 5x - 2) = -\frac 13 x - \frac 59 \\ x^3 &-\frac 53 x^2 &+ \frac 23 x \\ \hline &+ \frac 53 x^2 & - \frac 23 x &-1 \\ & +\frac 53 x^2 & - \frac{25}9 x &+ \frac{10}9 \\ \hline && + \frac{19}9 x &- \frac{19}9\end{alignat*}
Somit ist der Rest - und nur auf den kommt es beim euklidischen Algorithmus an - gleich \(19/9(x-1)\). Und im nächsten Schritt teilt man nur durch \((x-1)\). Den Faktor kann man später dazu hängen:
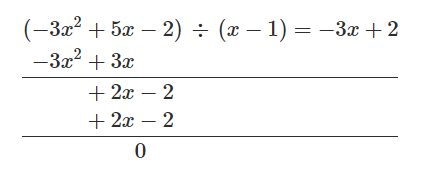
Latex: \begin{alignat*}{1} (-3x^2&+5x &- 2) \,\div \, (x-1) = -3x + 2\\ -3x^2 &+ 3x\\ \hline & +2x &-2 \\ &+2x & -2\\ \hline && 0\end{alignat*}
und es geht ohne Rest auf. Der größte gemeinsame Teiler ist also \(x-1\). Hier noch mal die vollständige Tabelle
$$\begin{array}{ccc} F & G& F \div G \\ \hline x^{3}−3x^{2 }+5x−3& x^{3}-1& 1 \\ x^{3}-1& -3x^2+5x - 2 & -\frac 13x - \frac 59\\ -3x^2+5x - 2& \frac{19}9(x - 1)& \frac{9}{19}(-3x + 2) \\ \frac{19}9(x - 1)& 0 \end{array}$$
Gruß Werner