e-Funktion Textaufgabe, In einer Tasse Kaffee....

Question

Hallo,

Aufgabe: In einer Tasse ist Kaffee mit der Anfangstemperartur von 90 C. Die Zimmertemperatur beträgt 20 C. Die momentane Änderungsrate der Temperatur des Kaffees(in C pro Minute) wird nächerungsweise beschrieben durch

g(t)= -10 *e^-1/7*t (t ≥ 0 , t in Minten),

a) Begründen Sie, dass die Funktion g nur negative Werte animmt und streng monoton wächst. Erläutern Sie, was das für den Abkühlungsprozess bedeutet.

Frage: Wie mache ich das?????Danke euch schon mal im Voraus.

Answer 1

Hallo,

g(t)= -10 * e^-1/7*t   (t ≥ 0 , t in Minten)

Die Funktion mit der Gleichung f(t) = e^k·t ist für negative k streng monoton fallend (mit dem Grenzwert 0 für t→∞) und der Funktionsterm nimmt nur positive Werte an.

Deshalb sind die Werte von g(t) (momentane Änderungsrate) alle negativ und ihre Beträge werden mit wachsendem t immer kleiner.  Außerdem hat g(t) für t→∞ den Grenzwert 0.

Die Temperatur des Kaffees nähert sich also - wenn man unterstellt, dass die Zimmertemperatur nur vernachlässigbar zunimmt - (von oben) beliebig dem Wert 20°C. Der Abkühlungsprozess wird dabei aber immer langsamer.

---

Nachtrag: Der untere Grenzwert 20°C ergibt sich aus physikalischen Gründen und findet Berücksichtigung bei dem mathematischen Modell in der Stammfunktion G(t) von g(t), die die Temperatur zur Zeit t angibt:

G(t) = ∫ -10 · e^{-1/7 · t}  dt  =  70 · e^{-1/7 · t} + c   mit   G(0) = 90  →  c = 20 

Gruß Wolfgang

Answer 2

g(t)= -10 *e-1/7*t (t ≥ 0 , t in Minuten),

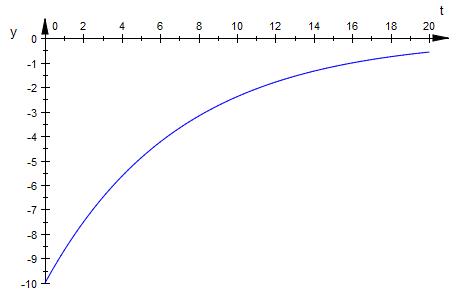
 a) Begründen Sie, dass die Funktion g nur negative Werte animmt

Die E-funktion hat stets positive Funktionswerte. Durch Multiplikation
mit -10 ist die Funktion stets negativ.

und streng monoton wächst.

1.Ableitung bilden und die Monotonie bestimmen.
g ´( t ) = -10 * e^(-1/7*t) * -1/7
g ´( t ) = 7 * e^(-1/7)
ist stets positiv also steigend.

Erläutern Sie, was das für den Abkühlungsprozess bedeutet.

Die Abkühlung nimmt immer weiter zu

Bemerkung : im Grunde geht es hier um das
Newtonsche Abkühlungsgesetz.
Überlicherweise wird dort die Temperatur der Flüssig-
keit ( nicht die Änderungsrate ) gegen die Zeit
betrachtet.
Zum Begreifen der physikalischen Vorgänge ist dies
wesentlich besser geeignet. und einfacher.