Lösung einer Steckbriefaufgabe

Question

Aufgabe:

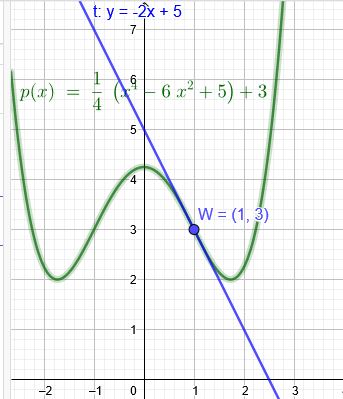
Bestimme eine ganzrationale Fkt, deren Graph zur y Achse symmetrisch ist. Dabei gilt dass bei (1|3) ein Wendepunkt ist und der Anstieg der Wendetangente -2 beträgt

Problem/Ansatz:

f(x)= ax^4+bx^2+c

Wie kann ich die Gleichungen aufstellen?

Answer 1

Aloha :)

Eine Gleichung 4-ten Gerades, achsensymmetrisch zur \(y\)-Achse hat die Form:$$y(x)=ax^4+bx^2+c$$$$y'(x)=4ax^3+2bx$$$$y''(x)=12ax^2+2b$$Von der Gesuchten wissen wir:$$\begin{array}{rcl}3 &=& y(1) &=&a+b+c\\-2 &=& y'(1) &=&4a+2b\\0&=&f''(1)&=&12a+2b\end{array}$$Wir lösen das Gleichungssystem mit dem Gauß-Verfahren:

$$\left(\begin{array}{r}a & b & c & =\\1 & 1 & 1 & 3\\4 & 2 & 0 & -2\\12 & 2 & 0 & 0\end{array}\right)\begin{array}{l}{}\\{} \\-4\cdot Z_1 \\-12\cdot Z_1\end{array}$$$$\left(\begin{array}{r}a & b & c & =\\1 & 1 & 1 & 3\\0 & -2 & -4 & -14\\0 & -10 & -12 & -36\end{array}\right)\begin{array}{l}{}\\{+\frac{1}{2}\cdot Z_2} \\{}\\-5\cdot Z_2\end{array}$$$$\left(\begin{array}{r}a & b & c & =\\1 & 0 & -1 & -4\\0 & -2 & -4 & -14\\0 & 0 & 8 & 34\end{array}\right)\begin{array}{l}{}\\{} \\{:(-2)}\\:8\end{array}$$$$\left(\begin{array}{r}a & b & c & =\\1 & 0 & -1 & -4\\0 & 1 & 2 & 7\\0 & 0 & 1 & 4,25\end{array}\right)\begin{array}{l}{}\\{+Z_3} \\{-2\cdot Z_3}\\{}\end{array}$$$$\left(\begin{array}{r}a & b & c & =\\1 & 0 & 0 & 0,25\\0 & 1 & 0 & -1,5\\0 & 0 & 1 & 4,25\end{array}\right)$$Die gesuchte Gleichung lautet daher:$$y(x)=\frac{x^4}{4}-\frac{3}{2}x^2+\frac{17}{4}$$

~plot~ x^4/4-1.5x^2+17/4 ; [[-3|3,3|0|10]] ~plot~

Answer 2

Du hast also den Punkt (1/3), dann gilt f'(1)=-2 und f"(1)=0.

Comments

Und wie lauten da die Gleichungen? Komme da auf kein Ergebnis.