Du kannst erstmal den Ausdruck sehr stark vereinfachen!
\(\int_0^1 ((4-2x)-(4-2x-4x^{-5x}))dx=4\cdot \int_0^1x^{-5x}dx \). So ein Integral ist nicht geschlossen lösbar. Du kannst das aber numerisch lösen.
Man kann es mit einem Computer direkt, auch nur numerisch, nach dieser Abbildung:
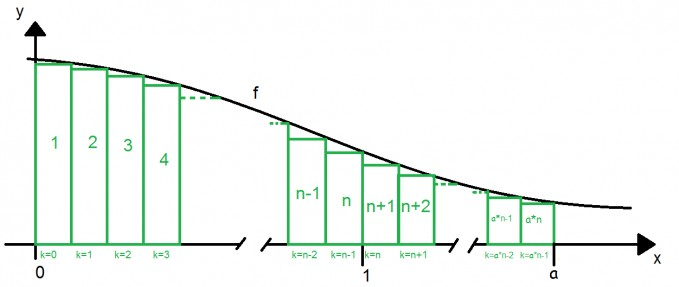
$$ A_k=\frac{1}{n}\cdot f(x),\text{ mit } x:=\frac{k}{n} $$
Dann hat man:
$$ \sum_{k=0}^{a\cdot n-1}{A_k}=\sum_{k=0}^{a\cdot n-1}{\frac{1}{n}\cdot f\Bigg(\frac{k}{n}\Bigg)}=\frac{1}{n}\cdot\sum_{k=0}^{a\cdot n-1}{ f\Bigg(\frac{k}{n}\Bigg)} $$
$$ f(x)=x^{-5x}\qquad : \int_0^1 x^{-5x}dx\\ \stackrel{n=1000}{\approx} \frac{1}{1000}\cdot \sum_{k=0}^{999} \Big( \frac{k}{1000}\Big)^{-5\cdot \frac{k}{1000}}\approx 3.9561$$
Also erhält man näherungsweise
$$ 4\cdot \int_0^1x^{-5x}dx\approx \underline{\underline{15,8244}} $$
Python-Code:
from math import*
n = int(input(' n = ')) #Einteilungsschritte
a = float(input(' a = ')) #Obergrenze
summe = 0
k=0 #Laufvariable k
while k<=a*n-1: #Es wird solange aufaddiert, bis diese Bedingung nicht mehr gilt
summe = summe+(k/n)**(-5*k/n)
k = k+1
print(summe/n)