Integral berechnen mittels Substitution ∫ x/(x^2 - 2)dx

Question

Aufgabe: Löse das Integral (Bild)

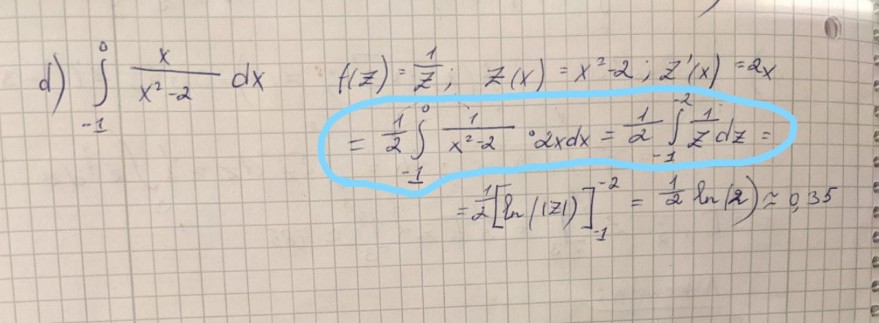
Text erkannt:

d) \( \int \limits_{-1}^{0} \frac{x}{x^{2}-2} d x \)
\( \begin{array}{l} f(z)=\frac{1}{z} ; \quad z(x)=x^{2}-2 ; z^{\prime}(x)=2 x \\ =\frac{1}{2} \int \limits_{-1}^{0} \frac{1}{x^{2}-2} \cdot 2 x d x=\frac{1}{2} \int \limits_{-1}^{-2} \frac{1}{z} d z= \\ =\frac{1}{2}[\ln (|z|)]_{-1}^{-2}=\frac{1}{2} \ln (2) \approx 0,35 \end{array} \)

Text erkannt:

d) \( \int \limits_{-1}^{0} \frac{x}{x^{2}-2} d x \)
\( \begin{array}{l} f(z)=\frac{1}{z} ; \quad z(x)=x^{2}-2 ; z^{\prime}(x)=2 x \\ =\frac{1}{2} \int \limits_{-1}^{0} \frac{1}{x^{2}-2} \cdot 2 x d x=\frac{1}{2} \int \limits_{-1}^{-2} \frac{1}{z} d z= \\ =\frac{1}{2}[\ln (|z|)]_{-1}^{-2}=\frac{1}{2} \ln (2) \approx 0,35 \end{array} \)

Problem/Ansatz:

Es handelt sich beim Bild um einen Lösungsansatz vom Professor.

Es geht bei mir nur um eine Verständnisfrage. Ich verstehe, dass wir x^2-2 mit z substituieren und 2x mit z'. Aber im blau markierten Bereich wird 2xdx mit dz substituiert was für mich keinen Sinn macht. Wie hängt das mit z zusammen?

Für jeden Kommentar wäre ich sehr dankbar!

Answer 1

Aloha :)

Willkommen in der Mathelounge... \o/

Schauen wir uns den Rechenweg mal an:$$I=\int\limits_{-1}^0\frac{x}{x^2-2}\,dx$$Im Nenner wird subsituiert:$$z(x)=x^2-2$$Das heißt für die Grenzen des Integrals:$$z(-1)=(-1)^2-2=-1\quad;\quad z(0)=0^2-2=-2$$Für das Differential bedeutet die Subsitution:$$\frac{dz}{dx}=z'(x)=2x\implies dx=\frac{dz}{2x}$$Nach der Substituiton haben wir also:$$I=\int\limits_{-1}^{-2}\frac{x}{z}\cdot\frac{dz}{2x}=\frac12\int\limits_{-1}^{-2}\frac{1}{z}\,dz=\frac12\left[\ln|z|\right]_{-1}^{-2}=\frac12\left(\ln(2)-\underbrace{\ln(1)}_{=0}\right)=\ln(2^{\frac12})=\ln(\sqrt2)$$