Nun, in beiden Aufgaben sind die jeweiligen Gleichungen bereits in Normalform.
Du weißt doch sicher, dass solche linearen Gleichungen Geraden im Koordinatensystem beschreiben. Die Lösung eines Gleichungssystems aus zwei solchen Gleichungen sind nun gerade die Koordinaten des Schnittpunktes dieser Geraden.
Zeichne also die den Gleichungen entsprechenden Geraden in ein Koordinatensystem ein und lies deren Schnittpunkt ab. Prüfe dann durch Einsetzen der abgelesenen Koordinaten in die Gleichungen, ob sich wahre Aussagen ergeben.
Für das erste Gleichungssystem ergibt sich folgendes Diagramm:
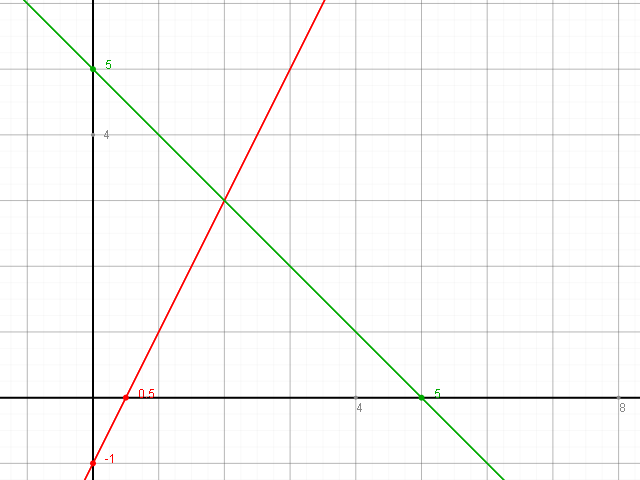
Die rote Gerade gehört zu der Gleichung y = 2 x - 1 , die grüne Gerade zu der Gleichung y = - x + 5
Die Koordinaten des Schnittpunktes sind x = 2 und y = 3, der Schnittpunkt ist also S ( 2 | 3 ).
Einsetzen der Koordinaten in die Gleichungen:
y = 2 x - 1 => 3 = 2 * 2 - 1 (wahre Aussage)
y = - x + 5 => 3 = - 2 + 5 (wahre Aussage)
Für x = 2 und y = 3 ergeben also beide Gleichungen wahre Aussgen. Also ist die Lösung richtig.
Bei dem zweiten Gleichungssystem machst du es nun genauso.