Aufgabe:
Ich möchte gerne mathematisch nachvollziehen,
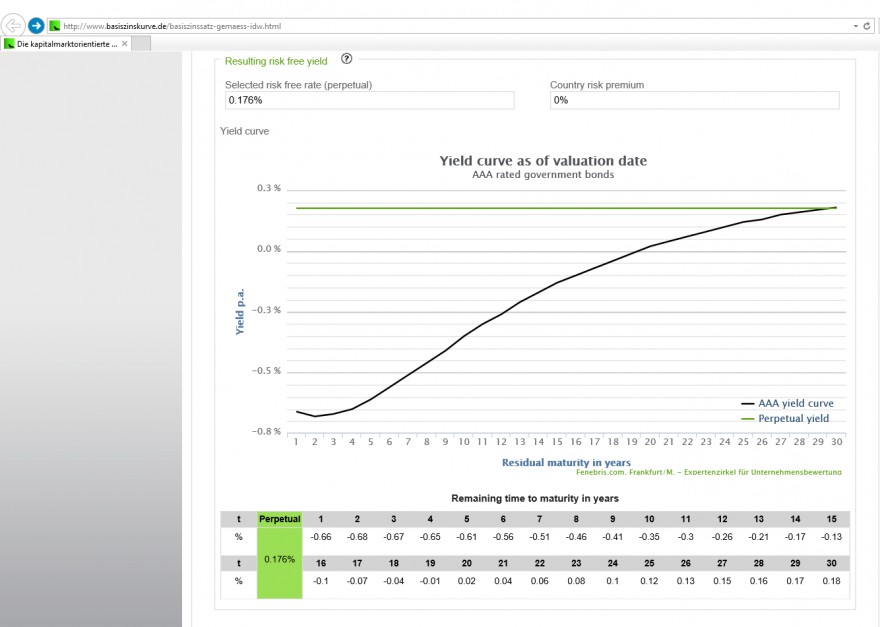
wie man auf den Basiszinssatz von -0,35 für eine Laufzeit vom 10 Jahren ab den 01.01.2020 kommt.
Jedoch scheint mir das selbst zu komplex. Hier der Link zur Website: http://www.basiszinskurve.de/basiszinssatz-gemaess-idw.html
Text erkannt:
4
kreepered
1
:
Problem/Ansatz:
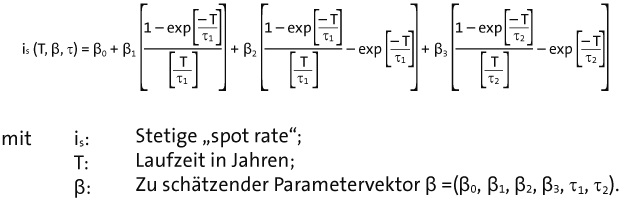
Text erkannt:
\( \mathrm{i}_{\mathrm{s}}(\mathrm{T}, \beta, \tau)=\beta_{0}+\beta_{1}\left[\frac{1-\exp \left[\frac{-T}{\tau_{1}}\right]}{\left[\frac{T}{\tau_{1}}\right]}+\beta_{2}\left[\frac{1-\exp \left[\frac{-T}{\tau_{1}}\right]}{\left[\frac{T}{\tau_{1}}\right]}-\exp \left[\frac{-T}{\tau_{1}}\right]\right]+\beta_{3}\left[\frac{1-\exp \left[\frac{-T}{\tau_{2}}\right]}{\left[\frac{T}{\tau_{2}}\right]}-\exp \left[\frac{-T}{\tau_{2}}\right]\right]\right. \)
mit Stetige, spot rate "; \( \mathrm{T}: \)
Laufzeit in Jahren; \( \bar{\beta}: \quad \) Zu schätzender Parametervektor \( \beta=\left(\beta_{0}, \beta_{1}, \beta_{2}, \beta_{3}, \tau_{1}, \tau_{2}\right) \)