Skalarprodukt: Kosinusform und Koordinatenform

Question

im Buch gab es die folgende Abbildung.

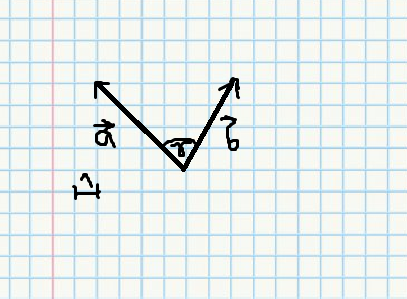
Habe versucht, a und b mit dem Geodreieck zu messen. Bin auf ungefähr 3 und 2 gekommen. Für den Winkel hätte ich 70 Grad.

nun soll ich das Skalarprodukt a*b mithilfe von Kosinusform und Koordinatenform berechnen:

Ansatz: Kosinusform: |a| * |b| * cos(gamma)

=> 9 * 4 * 0,34

= 12.31

Koordinatenform: (a1 a2) * (b1 b2) = a1b1 + a2b2

ich weiß überhaupt nicht, wie ich das machen soll, da ich nur ein "a" bzw. "b" habe??

ich bitte um Hilfe :(

* außerdem standen da noch die Zeichnungen: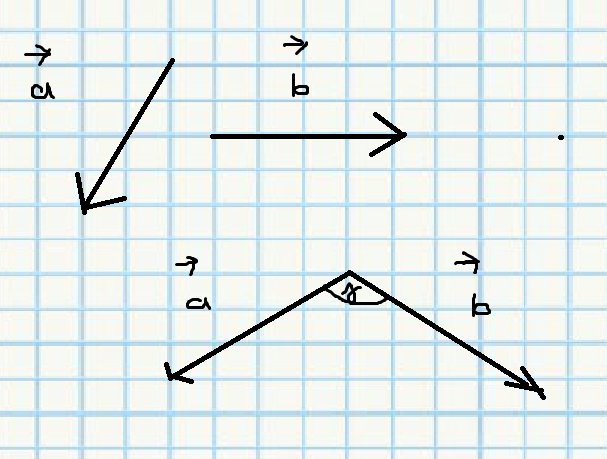

 ich weiß aber nicht, ob sie für die erste Aufgabe relevant sind, da ich unterschiedliche Zahlen raus bekomme, wenn ich diese messe(allerdings ist der Unterschied nicht extrem groß)...Denke also, dass es einzelne Aufgaben sind.

Ich brauche echt Hilfe mit der Aufgabe

Answer 1

Aloha :)

Du kannst die Vektoren aus der Skizze ablesen. Nimm dazu den gemeinsamen Startpunkt als Koordinatenursprung an$$\vec a=\binom{-4}{4}\quad;\quad\vec b=\binom{2}{4}$$$$\cos\gamma=\frac{\binom{-4}{4}\cdot\binom{2}{4}}{\sqrt{(-4)^2+4^2}\cdot\sqrt{2^2+4^2}}=\frac{-8+16}{\sqrt{32}\cdot\sqrt{20}}\approx0,3162\quad\Rightarrow\quad\gamma\approx71,57^o$$

Comments

hallo...ich weiß, dass die Frage von gestern ist, aber vielleicht können Sie mir an dieser Stelle noch helfen. Ich bräuchte Hilfe, bei der Zeichnung, wo sich die Vektoren nicht treffen.

Für a hätte ich -2 -4 gesagt, da es 2 nach links und 4 nach unten geht.

für b jedoch bin ich mir nicht sicher. Soll ich mich bei dem Ursprung nach a orientieren? Oder einfach da anfangen, wo b anfängt? dann wäre es 4 0, da es 4 Kästchen in die rechte Richtung sind und nichts nach unten oder oben

---

Soll ich mich bei dem Ursprung nach a orientieren?

Nein

einfach da anfangen, wo b anfängt? dann wäre es 4 0

das ist richtig. Du kannst einen Vektor frei verschieben. Also kann man \(b\) auch so verschieben, dass sein Anfang mit dem Anfang von \(a\) zusammen fällt.

---

Aloha ;)$$\vec a=\binom{-2}{-4}\quad;\quad\vec b=\binom{4}{0}$$Ein Vektor beschreibt eine Positionsänderung in einem Koordinatensystem. Das heißt, du kannst den Vektor innerhalb des Koordinatensystems verschieben. Das ist ein wichtiger Unterschied zu Punkten. Wenn du die Koordinaten eines Punktes angibst, z.B. \(A(1|2|3)\), dann ist diese Position fest.

---

ok vielen Dank:D

Answer 2

Hallo

 da das auf Kästchen gezeichnet ist und 2 Kästchen =1cm sind kannst du immer den Anfang als (0,0) nehmen und dann die Vektoren ablesen, im ersten Bild etwa a=(-2,2) b=(1,2) skalarprodukt 2 durch den Betrag teilen also durch √8*√5

 und dann den arccos  gibt 71,..°

genauso kannst du es mit allen Vektoren machen. Ob du Kästchen oder cm zählst ist egal, weil ja durch den Betrag geteilt wird

Gruß lul

Comments

hallo 1 Kästchen soll 1cm sein:)

mein Fehler, wenn man es nicht gut erkennen kann :(

aber danke sehr!!

Answer 3

Hallo,

ich vermute, Du sollst den Winkel \(\gamma\) zwischen den Vektoren mit Hilf des Skalarprodukts berechnen. Die Vektoren \(a\) und \(b\) erhältst Du über schlichtes Zählen der Kästchen. Es ist $$a = \begin{pmatrix} -4\\4 \end{pmatrix}, \quad b= \begin{pmatrix} 2\\4 \end{pmatrix} \\ a \cdot b = \begin{pmatrix} -4\\4 \end{pmatrix} \cdot \begin{pmatrix} 2\\4 \end{pmatrix} = -4 \cdot 2 + 4 \cdot 4 = 8$$ Die Beträge kann man nun über das Skalarprodukt oder den Pythagoras (was in 2D dassselbe ist) berechnen. Es ist $$|a| = \sqrt {a^2} = \sqrt{(-4)^2 + 4^4} = 4 \sqrt 2 \\ |b| = \sqrt{b^2} = \sqrt{2^2 + 4^2} = 2 \sqrt 5$$Und die Kosinusformel hast Du ja bereits angegeben. Da setzt man alles ein$$\begin{aligned}  a \cdot b &= |a| \cdot |b| \cdot \cos \gamma \\ 8 &= 4\sqrt 2 \cdot 2 \sqrt 5 \cdot \cos \gamma &&\left| \div 8 \sqrt{10}\right.\\ \frac 1{\sqrt{10}}&= \cos \gamma \\ \implies \gamma &= \arccos\left( \frac 1{\sqrt{10}}\right) \approx 71,6° \end{aligned}$$

Für den Winkel hätte ich 70 Grad.

passt ja zum Ergebnis