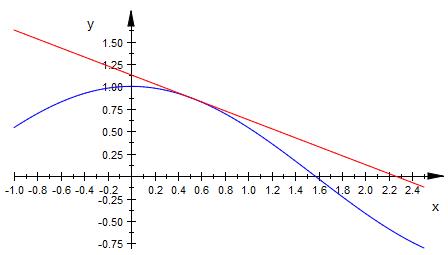
c) P((π/6|?)
f ( x ) = cos ( x )
f ´( x ) = - sin ( x )
x = π / 6 = 0.5236
f ( pi / 6 ) = 0.866
f ´( pi / 6 ) = -0.5
Tangente
t ( x ) = m * x + b
t ´ ( x ) = m
f ( x ) = t ( x ) | gleiche Koordinaten
f ´( x ) = t ´( x ) | gleiche Steigung
- sin ( pi / 6 ) = t ´( pi / 6 ) = m
m = -0.5
f ( x ) = t ( x ) = m * x + b
0.866 = -0.5 * pi / 6 + b
b = 0.866 + 0.2618
b = 1.128
t ( x ) = -0.5 * x + 1.128