Fast jeder hat im Grundschulalter das kleine Einmaleins so lange geübt, bis er es auswendig konnte. Wir müssen aber das Verständnis und die Automatisierung dieser Grundrechenart ‚Multiplizieren‘ deutlich voneinander trennen. Das Verständnis beruht auf der Einsicht: Multiplizieren ist die wiederholte Addition gleicher Summanden. Außerdem beinhaltet verstandene Multiplikation auch die Möglichkeit der Rückführung neuer Multiplikationsergebnisse auf bekannte. Zum Beispiel sei 5 · 7 = 35 bekannt, dann sollte 6 · 7 = 35 + 7 berechnet werden können.
Das „Zurückführen auf Bekanntes“ durchzieht das ganze Mathematiklernen, wie ein roter Faden und kann als eine Schlüsseltätigkeit der Mathematik bezeichnet werden. Es ist sicher von Vorteil, diese Schlüsseltätigkeit schon am Anfang der Schulzeit kennen zu lernen. Schließlich beinhaltet verstandene Multiplikation noch die Möglichkeit, Gesetze der Multiplikation einzusetzen: Kommutativgesetz, Assoziativgesetz und Distributivgesetz. Dabei müssen die Gesetze selbst nicht ihrem Wortlaut nach, sondern nur in ihrer praktischen Wirkung erlebt worden sein: 6 · 7 = 7 · 6 oder 7 · 6 = 7·(3+3) = 7·3 + 7·3 oder (7·2)·3 = 7·(2·3).
Dieses Erlebnis kann durch graphische Darstellungen ausgelöst werden z,B. 6·7=3·7+3·7:
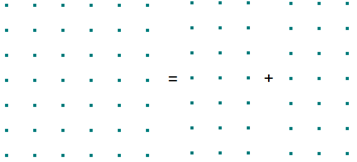
Mit einem derartigen Verständnis der Multiplikation braucht gar nicht das ganze Einmaleins gelernt zu werden, sondern lediglich das Verdoppeln, das Halbieren, das Multiplizieren mit 10 und die Folge der Quadratzahlen. Die auswendige Beherrschung der Quadratzahlen ist im späteren Verlauf des Lernens von Mathematik wieder einsetzbar, z. B., wenn es um das Wurzelziehen geht.
Aus diesen wenigen auswendig gewussten Bausteinen können alle weiteren Produkte des kleinen Einmaleins in ein bis zwei Schritten erschlossen werden, zum Beispiel:
1·7 = 7
2·7 = verdoppeln
3·7 = verdoppeln + 7
4·7 = 2×verdoppeln
5·7 = 7·10 halbieren
6·7 = 5·7 + 7
7·7 = Quadratzahl
8·7 = Quadratzahl + 7
9·7 = 10·7 - 7
10·7 = 70
Wer das Einmaleins auf diese Weise gelernt hat, wird in einem Kopfrechenwettbewerb vielen seiner Klassenkameraden vermutlich unterlegen sein, welche die Ergebnisse reflexartig hervorbringen. Aber im weiteren Verlauf des Mathematikunterrichtes kommen neue Rechenarten mit Potenzen, Wurzeln, und Logarithmen hinzu, die jeweils eigenen Rechenregeln gehorchen.
Die Flut all dieser vielen Regeln und Gesetze ist dann irgendwann so groß, dass einige davon wieder vergessen werden. Da ist es sehr von Nutzen, Neues auf Bekanntes zurückführen zu können und erlebt zu haben, wie diese Schlüsseltätigkeit das Auswendiglernen weitgehend überflüssig macht.