Als Lehrer ist man sozusagen "berufsmäßig" auf die Annahme festgelegt, dass Lernen möglich ist. Doch wie ist Lernen möglich? Und was ist überhaupt "Lernen"? Seitdem Platon diese Frage vor fast 2400 Jahren erstmalig aufgeworfen hat, sind wir mit einer ungeheuren Vielzahl möglicher Antworten auf diese Fragen konfrontiert, ohne dass sich bislang eine einheitliche Überzeugung dazu durchgesetzt hätte. Der hier skizzierte Ansatz einer semiotischen Lerntheorie geht davon aus, dass jede Kommunikation und jede Repräsentation von Wissen offenbar auf Zeichen angewiesen ist. So liegt es nahe, deren mögliche Rolle in Lernprozessen einmal genauer zu untersuchen.
In Platons klassischem ‚Dialog Menon‘ bezweifelt Menon gegenüber Sokrates, dass nur aus vorhandenem Wissen neues Wissen entstehen kann, ohne dass Fakten außerhalb des vorhandenen Wissens hinzugefügt werden. Bei sorgfältiger Betrachtung des von Platon geschilderten Gedankenaustausches zwischen Sokrates, Menon und einem Knaben, entdeckt man allerdings die Einführung eines für den Knaben neuen Begriffes durch Sokrates. Es handelt sich um den Begriff der ‚Diagonale als Strecke, die ein Quadrat in der Fläche halbiert‘. Also sind Menons Zweifel eigentlich nicht beseitigt – obwohl Platon ihn überzeugt sehen möchte.
Dabei ist es heute eigentlich ganz einfach, zu begründen, dass neues Wissen auf der Basis vorhandenen Wissens erzeugt werden kann. Im Grunde fordert fast jede im Mathematikunterricht an die Schüler*innen gestellte Aufgabe genau dieses. So ist eben meistens eine Frage zu beantworten, deren Antwort unbekannt ist. Wenn diese Frage nicht in der Sprache der Mathematik vorliegt, ist sie zuerst in die Sprache der Mathematik zu übersetzen. Anschließend ist (unter Einsatz von heuristischen Prinzipien und Methoden) durch Anwendung mathematischer Regeln, Sätze und Gesetze die mathematisch formulierte Frage in andere gleichbedeutende Repräsentationen zu überführen. Dabei hofft man auf eine Repräsentation zu stoßen, deren Wahrheitsgehalt entweder dem/r Aufgabenlöser*in gesichert erscheint oder durch eine Probe bestätigt werden kann.
An dieser Stelle wird klar, dass das Gewinnen mathematischen Wissens Einiges voraussetzt: Kenntnis und Verfügbarkeit notwendiger Regeln, Sätze und Gesetze sowie heuristischer Prinzipien und Methoden. Und manchmal ist zusätzlich ein Geistesblitz (ein genuin kreativer Gedanke) erforderlich.
Eine Beispielaufgabe:
Zwei Strahlen g und h beginnen in A. Auf h liegt ein Ziel P. Gesucht ist ein Streckenzug von A nach P aus drei Strecken gleicher Länge, von denen eine auf g, eine auf h und eine dritte zwischen g und h liegt.
Eine Übersetzung in die Sprache der Mathematik ist hier die Übersetzung des Aufgabentextes in eine Skizze.
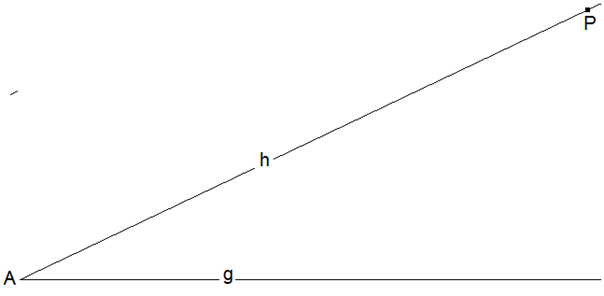
Darüber hinaus muss die heuristische Methode des Weglassens einer Bedingung verfügbar sein. Man verzichtet zunächst darauf, den Streckenzug aus drei Strecken gleicher Länge in P enden zu lassen.
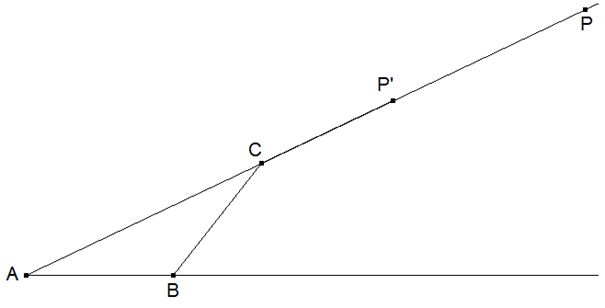
Nun ist die Kenntnis der zentrischen Streckung einschließlich derer Eigenschaften erforderlich. Das Dreieck BP’C ist so zu strecken, dass P’ auf P fällt. Dazu bedarf es der heuristischen Methode der Einführung von Hilfslinien (zunächst BP’ und dann B’P als Bild von BP‘).
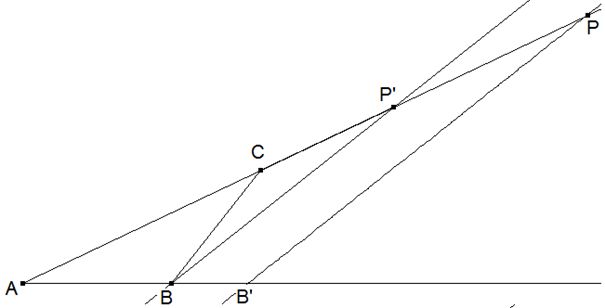
Der Abstand des Bildpunktes B‘ vom Streckzentrum A ist die gesuchte Länge jeder Strecke des Streckenzuges AB’C’P.
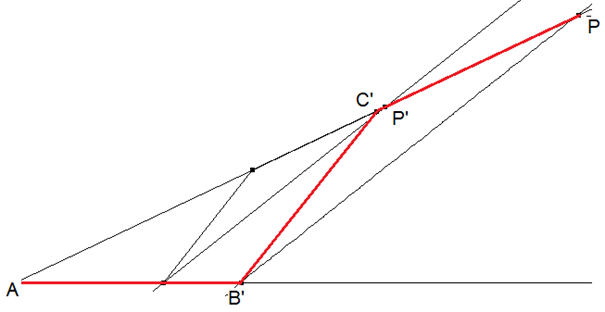
In dieser Lösung wird – wie in jeder Lösung - deutlich, dass die Gewinnung mathematischen Wissens auf Zeichen (im peircschen Sinne) angewiesen ist. Für Charles Sanders Peirce sind Zeichen bereits die Worte des Aufgabentextes (schriftlich oder mündlich). Das Vorhandensein von Zeichen und der Umgang damit und die dabei gesammelten Erfahrungen sowie die Vorstellung von ihrer Bedeutung sind nach Peirce die wesentlichen Erkenntnisbedingungen. Und Lernen ist aus semiotischer Sucht nichts anderes, als die Entwicklung von Erkenntnisbedingungen.