Hallo solevita,
Damit \(A'\) der Spiegelpunkt von \(A\) an \(E\) ist, müssen zwei Bedingungen erfüllt sein:
1.) Der Differenzvektor \(d=A'-A\) muss kolinear zum Normalenvektor \(n\) von \(E\) sein.
2.) Der Mittelpunkt \(M_{AA'}\) muss auf \(E\) liegen.
Der Differenzvektor \(d\) ist $$d = A'-A = \begin{pmatrix}1\\ -4\\ -4\end{pmatrix} - \begin{pmatrix}5\\ 4\\ 8\end{pmatrix} = \begin{pmatrix}-4\\ -8\\ -12\end{pmatrix}$$Und da $$E: \space \begin{pmatrix}1\\ 2\\ 3\end{pmatrix} \cdot x = 9 \implies n = \begin{pmatrix}1\\ 2\\ 3\end{pmatrix}$$ ist $$d = -4 \cdot n$$die beiden Vektoren sind kolinear, die 1. Bedingung ist erfüllt. Die Mitte \(M_{AA'}\) ist$$M_{AA'} = \frac 12 \left( A' + A\right) = \frac 12 \left( \begin{pmatrix}1\\ -4\\ -4\end{pmatrix} +\begin{pmatrix}5\\ 4\\ 8\end{pmatrix} \right) = \begin{pmatrix}3\\ 0\\ 2\end{pmatrix}$$Und die Koordinaten von \(M_{AA'}\) erfüllen die Ebenengleichung:$$1 \cdot 3 + 2 \cdot 0 + 3 \cdot 2 = 9$$Also ist \(A'\) das Spiegelbild von \(A\) an \(E\).
So sieht das in 3D aus:
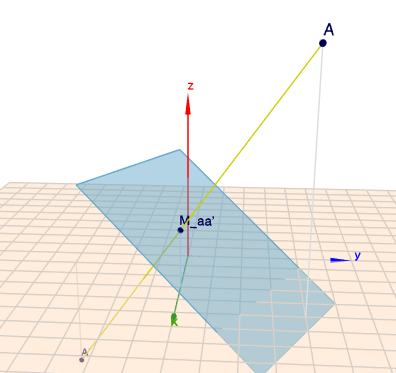
(klick auf das Bild)