Aufgabe
Bastelarbeit im Kindergarten
Als Werkarbeit in einem Kindergarten sollen Katzenköpfe aus Modelliermasse gestaltet werden. Als Vorlage dazu dient eine Ausstechform. Die Begrenzungslinien dieser Ausstechform können durch die Graphen der Funktionen \( f \) und \( g \) beschrieben werden:
\( f(x)=-0,5 \cdot x^{4}+1,8 \cdot x^{2}+5 \)
\( g(x)=0,8 \cdot x^{2}+1 \)
\( x, f(x), g(x) \ldots \) Koordinaten in \( \mathrm{cm} \)
Die Graphen dieser Funktionen sind in der nachstehenden Abbildung dargestellt.
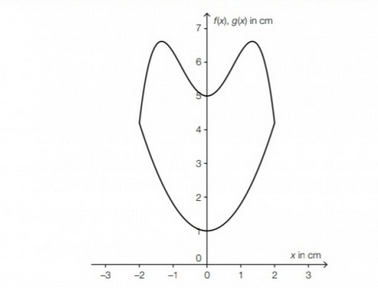
a) 1) Argumentieren Sie mithilfe der Funktionsgleichungen, dass der Graph der Funktion \( f \) die obere Begrenzungsinie und der Graph der Funktion \( g \) die untere Begrenzungslinie beschreibt (und nicht umgekehrit).
b) Modeliliermasse erhält man in quaderförmigen Packungen mit folgenden Maßen:
(B) \( 95 \mathrm{mm} \times(\mathrm{T}) 25 \mathrm{mm} \times(\mathrm{H}) 200 \mathrm{mm} \)
1) Berechnen Sie das Volumen einer Packung Modelliermasse in \( \mathrm{cm}^{3} \).
Jedes Kind soll mithife der Form einen 2 cm dicken Katzenkopf ausstechen können.
2) Berechnen Sie, wie viele Packungen Modeliermasse man mindestens benötigt, damit alle 24 Kinder der Gruppe jeweils einen Katzenkopf basteln können.
Problem/Ansatz:
Ich bräuchte nur b2) ,warum muss man beim volumenberechnung des katzenkopfes anfangs 2*dem integral von - 2,2?
b1) Volumen einer Packung Modelliermasse in cm":
\( V=9.5 \cdot 2,5 \cdot 20=475 \)
Das Volumen einer Packung Modelliermasse beträgt \( 475 \mathrm{cm}^{3} \)
b2) Volumen eines modellierten Katzenkoptes in \( \mathrm{cm}^{3}: V=2 \cdot \int \limits_{-2}^{2}[f(x)-g(x)] d x=\frac{448}{15}=29,87 \)
Volumen von 24 modelierten Katzenköplen in \( \mathrm{cm}^{3}: 24 \cdot \frac{448}{15}=716,8 \) Da eine Packung \( 475 \mathrm{cm}^{3} \) beinhaltet, benötigt man also mindestens 2 Packungen Modelliermase