Aber kannst du mir erklären, dass mit a,b,c stehen paarweise senkrecht aufeinander?
Ich habe dem Bild oben die drei Vektoren \(a\), \(b\) und \(c\) hinzu gefügt:
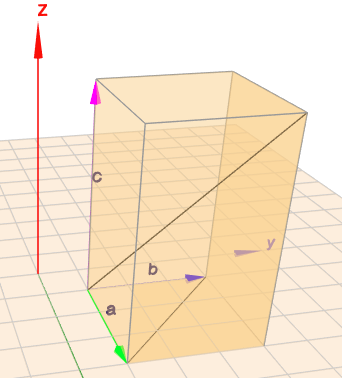
'paarweise senkrecht' heißt, dass \(a\) senkrecht auf \(b\) steht und \(b\) senkrecht auf \(c\) und \(c\) senkrecht auf \(a\). In einem Quader stehen alle nicht parallelen Seiten senkrecht zu einander. 'paarweise' bedeutet, dass man aus den drei Vektoren zwei entnimmt, und diese beiden stehen senkrecht auf einander. Das gilt für jedes Paar.
Und da das Skalarprodukt zweier senkrecht zu einander stehnder Vektoren \(=0\) ist, komme ich dann zu obiger Vereinfachung des Terms.