Aufgabe:
Ein Fußballtor ist \( 7,32 \mathrm{m} \) lang und \( 2,44 \mathrm{m} \) hoch. Paul trifft beim Elfmeterschießen auf die Stangen im linken oberen Eck des Tors, dem "Kreuzeck" (Punkt T). Gehen Sie davon aus, dass die Bahn des Balls geradlinig verläuft und vernachlässigen Sie die Größe des Balls und die Breite der Stangen des Tors.
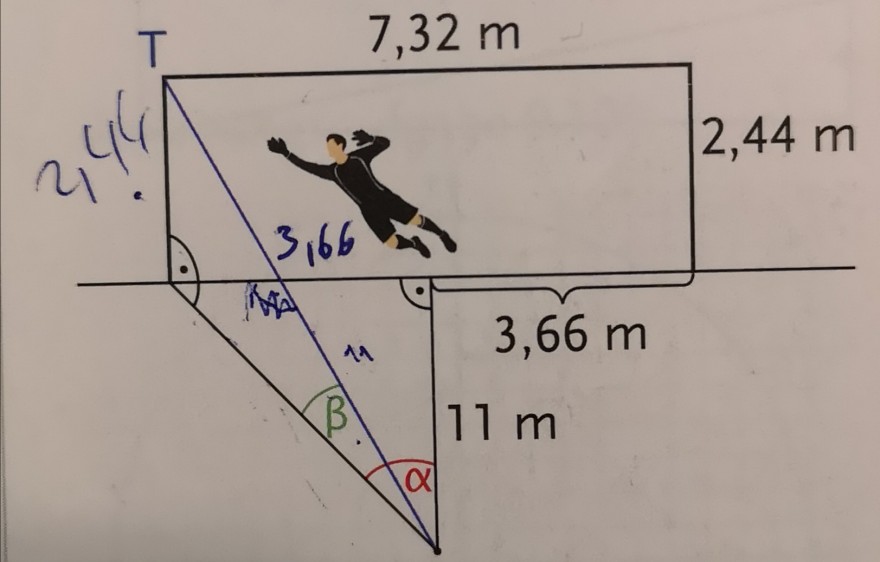
a) Beschreiben Sie die in der Grafik eingezeichneten Winkel \( \alpha \) und \( \beta \)
b) Berechnen Sie die Winkel.
Problem/Ansatz:
Ich verstehe nicht warum bei b) man den β Winkel so ausrechnet :tan:2,44/wurzel aus (11^2+3.66^2), also warum wurzel aus?
Bitte um hilfe
