Berechnen Sie die Koordinaten des Punktes S und die Größe des Reflektionswinkelns.

Question

Aufgabe:

In einem gedachten kartestischen Koordinatensystem befindet sich ein Spiegel in der Ebene E mit der Gleichung x-z = -20 . Vor dem Spiegel befindet sich eine Lichtquelle im Punkt P (5;-1;1). Ein vom Punkt P ausgehender Lichtstrahl wird an der Spiegelebene E im Punkt S reflektiert. Der reflektierte Strahl verläuft durch den Punkt R (-7;5;-35).

Berechnen Sie die Koordinaten des Punktes S und die Größe des Reflektionswinkelns.

Answer 1

Planzeichnung:

Ich würde den Spiegelpunkt R' von R gespiegelt an Ebene E berechnen (Normalenvektor).

Dann bilden PR' den Lichtstrahl ab auf den es ankommt, dh. den Strahl der an der Ebene im Punkt S  reflektiert wird und der auf R trifft. Sollte dann so aussehen 

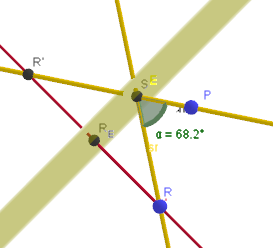
R_E:=((-31), 5, (-11))

S hast Du ja schon....

Add: Ach - das nein -  das S zu meinem Plan ist S=(-15,1,5)

Comments

Wie berechnest du S?

---

Wie berechnest du S?

Man schneidet die Gerade durch R' und P mit der Ebene E und erhält den Punkt S.

Answer 2

Es wundert mich etwas, dass die wetteiferndsten Antworter hier alle schweigen.

Nur so viel: einfallender und reflektierter Strahl befinden sich in einer gemeinsamen Ebene, die auf der Spiegelebene senkrecht steht.

Bekommst du eine Gleichung dieser senkrechten Ebene hin?

Comments

Ich habe S ermittelt mit (15| -1| -9)

Das haut aber nicht mit den Lösungen von meiner Lehrerin: S (15|-1|5) überein.

α ist übrigens 34,1°.

Ich habe eine Gerade gebildet, aus S und SR als Richtungsvektor, und den Schnittwinkel mit der Ebene berechnet, jedoch erhalte ich nicht den geforderten Wert.

---

Keiner der beiden vorgeschlagenen S liegt in der angegebenen Ebene E.

---

Es geht ja nicht darum ob sie in der Ebene liegen. Ein es geht um den gespiegelten Punkt, welcher genauso weit wie der "Ausgangspunkt" von der Ebene entfert ist, bloß auf der "anderen Seite" liegt.