Also die erste Folge ist ja ähnlich wie eine Funktion definiert. Du könntest auch f(x) = (x+1)/(2^x) schreiben. Das wäre nicht genau dasselbe, weil bei Folgen n bzw. x nur natürliche Zahlen annehmen kann. Du dürfest also nicht f(2,5) oder sowas berechnen, halt nur f(1), f(2), f(3), ...
Als Funktion würde das so aussehen:
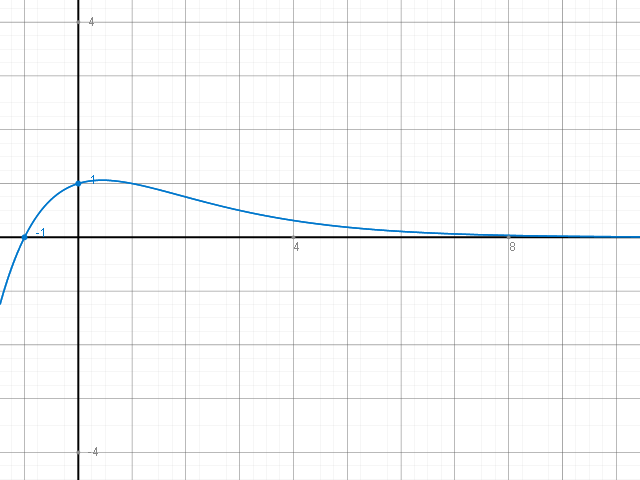
Du musst jetzt halt drauf achten, dass die Definitionswerte bei einer Folge nur 1,2,3, ..., also die natürlichen Zahlen sind. D.h. alle was zwischen 1,2 und 2,3 und 3,4 und ... ist, gehört nicht zur Folge. In der Skizze kannst du dir dann Punkte denken bei x = 1, 2, 3, 4, ... und dazwischen ist nichts.
Bei der zweiten Folge musst du die Folgenglieder nacheinander ausrechnen, ja.
Es ist a1 = 2.
Dann ist nach der Vorschrift
a2 = a1/2 + 1/a1 = 2/2 + 1/2 = 3/2
a3 = a2/2 + 1/a2 = (3/2)/2 + 1/(3/2) usw.
Zur Skizze musst du das auch nur noch in ein Koordinatensystem einzeichnen, als Punkte. Dabei ist der Index bei den Folgen, also bei a2 z.B. 2, dein "x" in dem Koordinatensystem und den Wert, den das Folgenglied ergibt, dein "y". Also x = 2, y = 3/2. x = 3, y = (3/2)/2 + 1/(3/2) usw.