Die Gleichung für \(a_n\) ist also
$$a_n = \frac{1+ 2n^{2}}{ n^{2} - 2} $$
und daher auch nur von \(n\) abhängig. Setzte also das \(n\) beginnend mit \(1\) einfach ein. Das Ergebnis sollte sein:
$$\begin{array}{c|c}n & a_n \\ \hline 1& -3\\ 2& 4.5\\ 3& 2.714285714\\ 4& 2.357142857\\ 5& 2.217391304\\ 6& 2.147058824\\ 7& 2.106382979\\ 8& 2.080645161\\ 9& 2.063291139\\ 10& 2.051020408\\ 11& 2.042016807\\ 12& 2.035211268\\ 13& 2.02994012\\ 14& 2.025773196\\ 15& 2.022421525\end{array}$$ Bem.: die Dezimalzahlen sind gerundet.
Nachtrag:
als Kurve sieht das so aus:
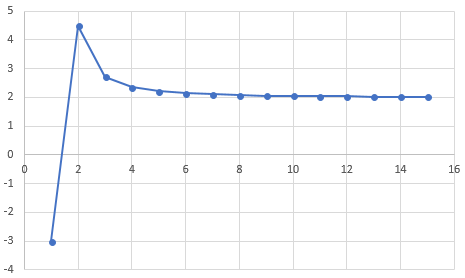
und \(a_n\) kann man nach einer Polynomdivision auch schreiben als
$$a_n = \frac{2n^{2} + 1}{ n^{2} - 2} = 2 + \frac{5}{n^2 - 2}$$ folglich ist $$\lim_{n \to \infty} a_n = \lim_{n \to \infty} \left( 2 + \frac{5}{n^2 - 2} \right) = 2$$