Lineare Iterierte Abbildungen über Waldbäume

Question

In einem Wald werden jedes Jahr k Bäume neu gepflanzt und 25% des bisherigen Gesamtbestandes gerodet. Zusätzlich verringert sich der bisherige Baumbestand wegen Schädlingsbefalls jährlich um weitere 5%. (Nehmen Sie der Einfachheit halber an, die neuen Bäume seien im Jahr der Pflanzung vom Befall noch nicht betroffen).

a) Wie entwickelt sich die Anzahl der Bäume über die Jahre? Geben Sie sowohl eine rekursive, als auch eine nicht rekursiv definierte Folge an.

b) Zeichnen Sie den Graphen der Iterationsfunktion und illustrieren Sie graphisch die Entwicklung des Baumbestands für verschiedene Anfangswerte. Wie hängt das dynamische Verhalten von k ab?

c) Wie viele Bäume sind nach sehr langer Zeit zu erwarten (näherungsweise nach unendlich vielen Jahren)? Begründen Sie Ihre Aussage mit dem Grenzwert der nichtrekursiv definierten Folge. (Zur Probe: für k = 300 erwarten wir 1000 Bäume.)

Unten habe ich einen Ansatz für a), bin mir aber nicht sicher. Bei b) und c) weiß ich nicht wie ich beginnen soll, da diese Thematik für mich neu und schwierig ist. Ich hoffe Ihr könnt mir helfen und verbleibe ,





 

Comments

Ich möchte meine Zeichnung korrigieren! Dort wo 0,75 steht, einfach 0,70 vorstellen bzw. ersetzen.

,



PS: Ich bin mir zwar nicht sicher, aber ich denke dann müsste es stimmen und wenn nicht, dann bitte ich um eine Berichtigung.

 

---

Welche Werte nutzt man für die Skizze?

Answer 1

hi

b)

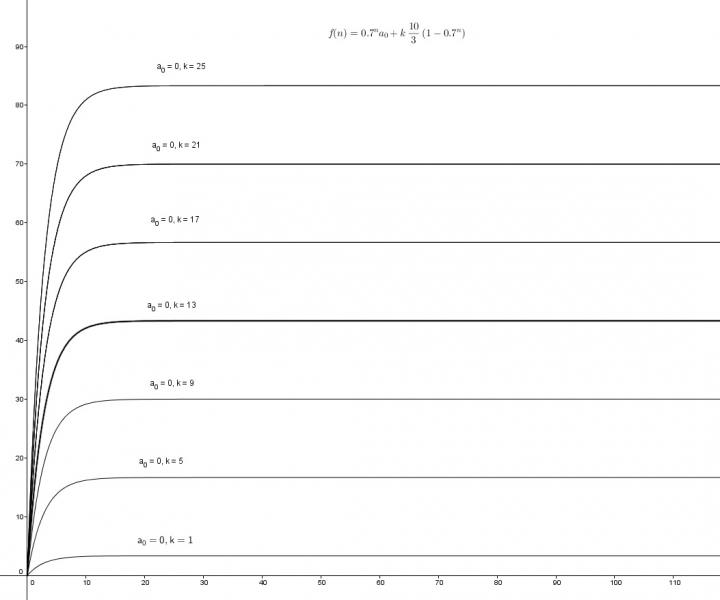
um die werte zu bekommen, können wir die reihe in eine funktionsgleichung umformen

$$\sum_{i=0}^{n-1}0.7^i = 1 + 0.7 + 0.7^1 + ... + 0.7^{n-1} = \frac{1-0.7^n}{0.3} = \frac{10}{3}(1-0.7^n)\\ a_n = 0.7^na_0 + k\sum_{i=0}^{n-1}0.7^i = \\ a_n = 0.7^na_0 + k\frac{10}{3}(1-0.7^n)$$

c)

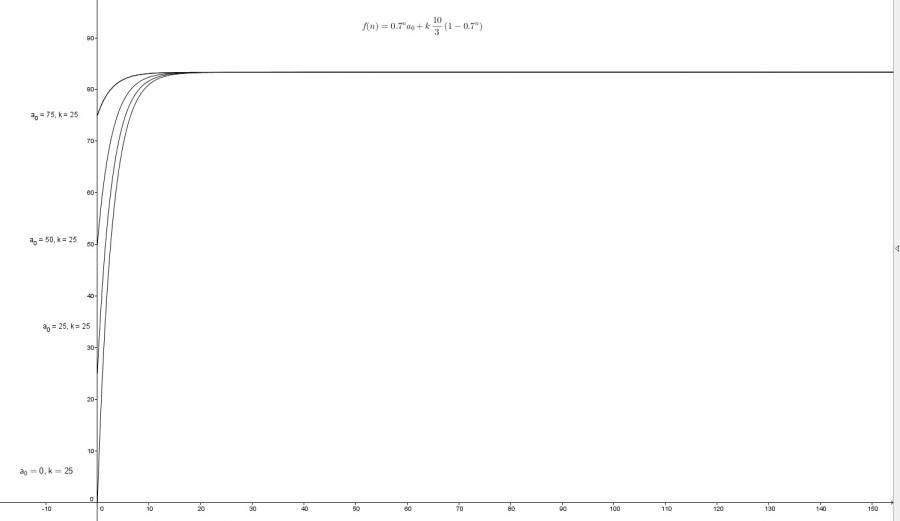
Den Grenzwert bekommen wir über die Grenzwertbildung einer geometrischen Reihe.

$$\lim_{n \to \infty} \left(0.7^na_0 + k\sum_{i=0}^{n-1}0.7^i \right) = \\ k \frac{1}{1-0.7} = \frac{10}{3}k$$

Comments

Erst einmal ein großes Lob für deine schnelle Antwort! Du hast es schön Übersichtlich dargestellt, wodurch man den Inhalt und die Herangehensweise besser verstehen kann. Bevor ich dir den Stern vergebe, möchte ich nur noch wissen, ob Aufgabe a) (von mir berechnet) richtig ist.

---

Ich denke, Aufgabe a) ist richtig. ich habe deine rechnung auf einem blatt papier nachvollzogen und keine fehler gefunden.

---

O.K. alles klar :) Dann bedanke ich mich für deine Unterstützung!