Hallo Lorenzo,
Der Punkt \(S\) ist der Schnittpunkt der Geraden \(g_{AS}\) und \(g_{BS}\). Die Geradengleichung (Punkt-Richtungs-Form) durch \(CS\) bekommt man mit dem Punkt \(C\) und der Richtung des Normalenvektors \(\vec n\) der Ebene \(E\)$$E: \space 2x+2y-z=9 \quad \to \vec n = \begin{pmatrix}2\\ 2\\ -1\end{pmatrix}$$Nun berechnest Du jeweils den Schnittpunkt von jeder der drei Geraden mit \(E\) und bekommst so die Punkte \(A\), \(B\) und \(C\). Zur Kontrolle:$$S = \begin{pmatrix}17\\ 12\\ 4\end{pmatrix}, \quad A = \begin{pmatrix}5\\ -3\\ -5\end{pmatrix}, \quad B= \begin{pmatrix}-1\\ 9\\ 7\end{pmatrix}, \quad C= \begin{pmatrix}7\\ 2\\ 9\end{pmatrix}$$Und noch eine Skizze in Geoknecht3D zur Illustration und besseren Verständnis:
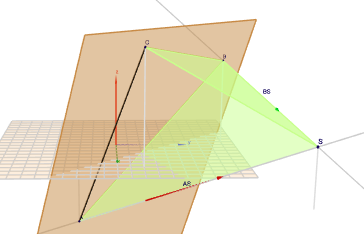
(klick auf das Bild, dann kannst Du die Szene mit der Maus drehen)
Falls irgendwas nicht klar ist, oder Du weißt nicht wie es geht, oder vielleicht kannst Du auch mit der Skizze nichts anfangen, so melde Dich bitte