Hallo liebe Lounge,
ich hätte gerne einen Kommentar von euch zu folgender Herleitung des Flächeninhalts eines beliebigen Dreiecks. Ist diese stringent?
z.Z. Flächeninhalt Dreieck AD=0.5*g*h
Voraussetzung: Flächeninhalt eines Rechecks AR=a*b=g*h
Betrachtet man zunächst spitzwinklige Dreiecke und ihren Grenzfall, das rechtwinklige Dreieck, so liegen die Höhen immer innerhalb des Dreiecks (bzw. auf einer der Katheten).
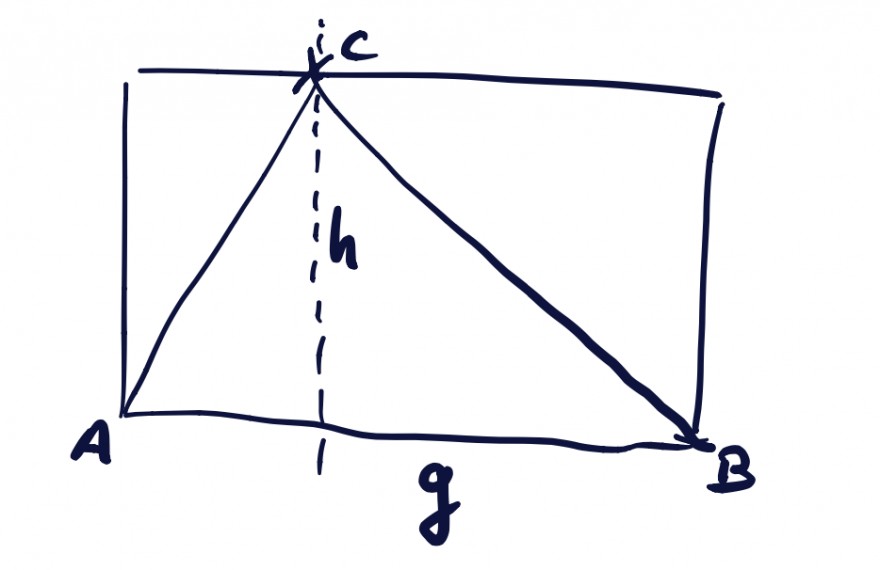
Die Höhe teilt das Dreieck in zwei Dreiecke. Diese sind jeweils kongruent zu dem Dreieck, welches das Rechteck auf der entsprechenden Seite komplettiert.
AR= g*h, woraus folgt, dass 2*AD=AR, somit AD=0.5*g*h.
Bleibt die Formel zu zeigen für stumpfwinklige Dreiecke:
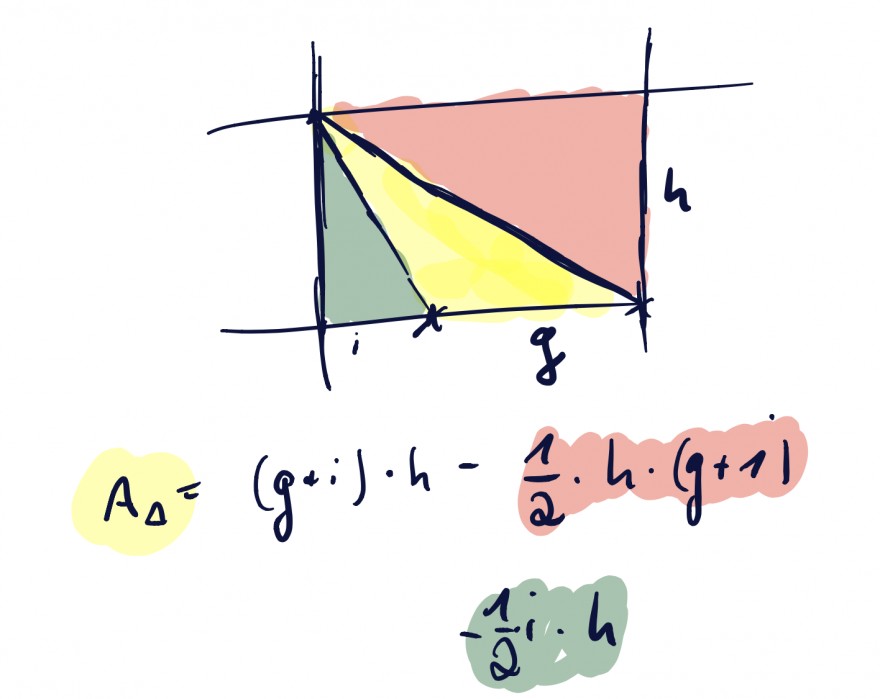
= 0.5*h*g.
Anm. Für rechtwinklige Dreiecke ergeben sich sofort zwei kongruente Dreiecke im Rechteck, sodass die Formel folgt.
Was haltet ihr davon?
Insbesondere die Frage, ob man die Fallunterscheidung machen muss...