Liebe Lounge, es geht um den Beweis für den Flächeninhalt eines Parallelogramms, ohne dass der Flächeninhalt eines Dreiecks bekannt ist.
Bekannt ist, dass der Flächeninhalt eines Rechtecks, AR=a*b gilt.
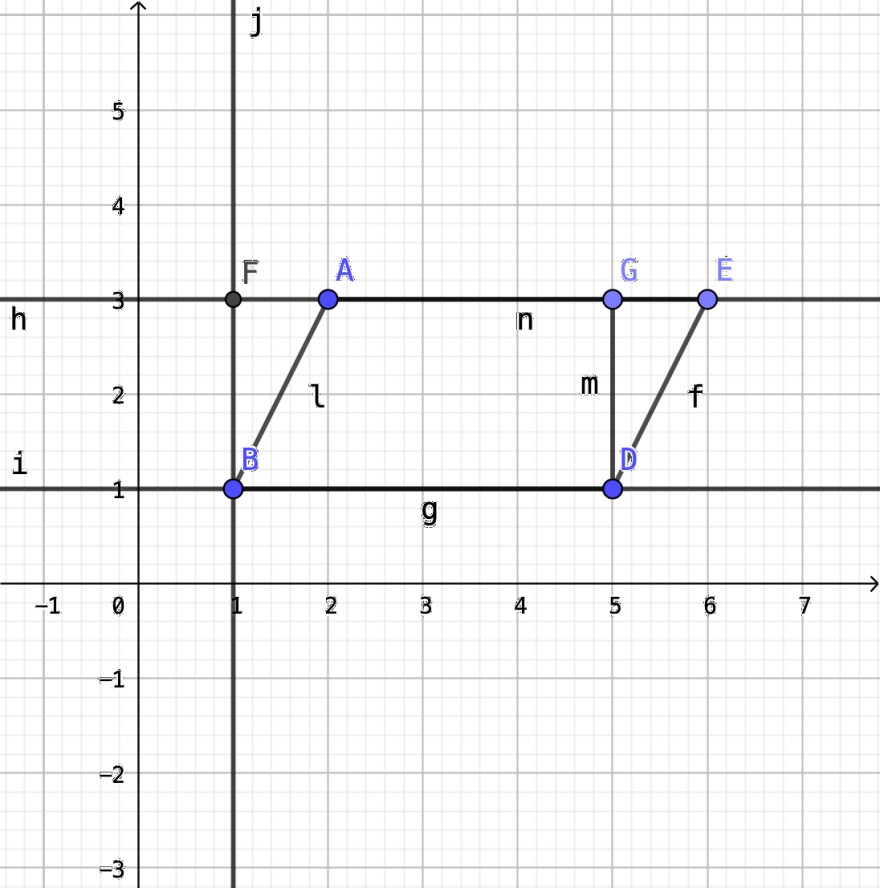
Hat man jetzt ein beliebiges Parallelogramm mit der Grundseite g und der Höhe m.
Legt man nun eine Gerade durch E und A und eine Gerade durch B und D. Nun fällt man das Lot von B auf die Gerade durch A und E.
Wenn man jetzt zeigt, dass die Dreiecke BAF und DEF kongruent sind, dann ist der Flächeninhalt des Parallelogramms AP: AP=g*m , wobei m die Höhe ist.
Die beiden Dreiecke stimmen in den Strecken BF und DG überein, da dies gerade der Abstand der beiden parallelen Geraden ist. Sie stimmen in den Strecken BA und DE überein, da so gerade das Parallelogramm definiert ist. Ferner haben sie beide einen Rechten Winkel bei AFB und bei EGD.
Da dies der Winkel ist, der der größeren Seite gegenüberliegt, sind die beiden Dreiecke nach Ssw kongruent.
Damit wäre die Formel bewiesen.
Passt das so?
Vielen Dank!