Vom Duplikat:
Titel: Der Kosinus und der Tangens (Aufgaben 13)
Stichworte: kosinus,tangens,sinus
Karl beobachtet von seiner Luftmatratze aus ein Flugzeug. Zunächst sieht er es unter dem Winkel Alpha = 60°, eine Minute später unter dem Winkel Beta = 25°. Wie weit ist das Flugzeug in dieser Zeit geflogen, wenn man von einer Flughöhe von 10 km über dem Meeresspiegel ausgeht?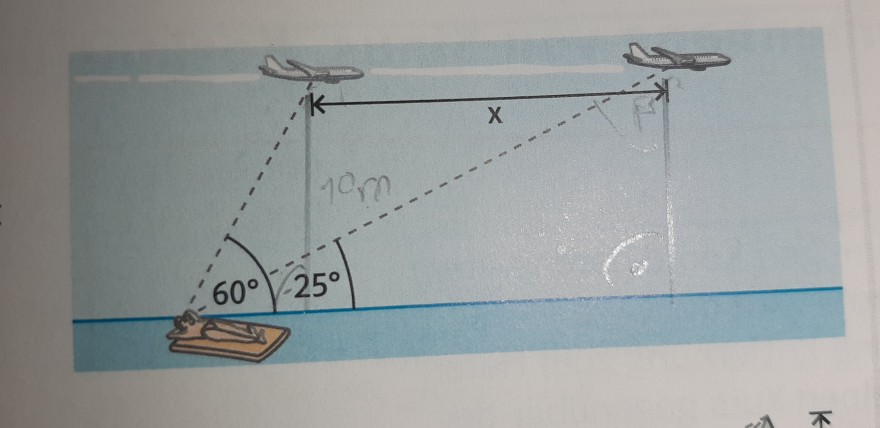
Text erkannt:
\( \frac{1}{x}, \quad k=-\frac{\Delta x}{x} \)
\( \frac{i^{\prime} 60^{\circ}}{25^{\circ}} \cdot-\frac{-5^{n}}{25^{\circ}} \)