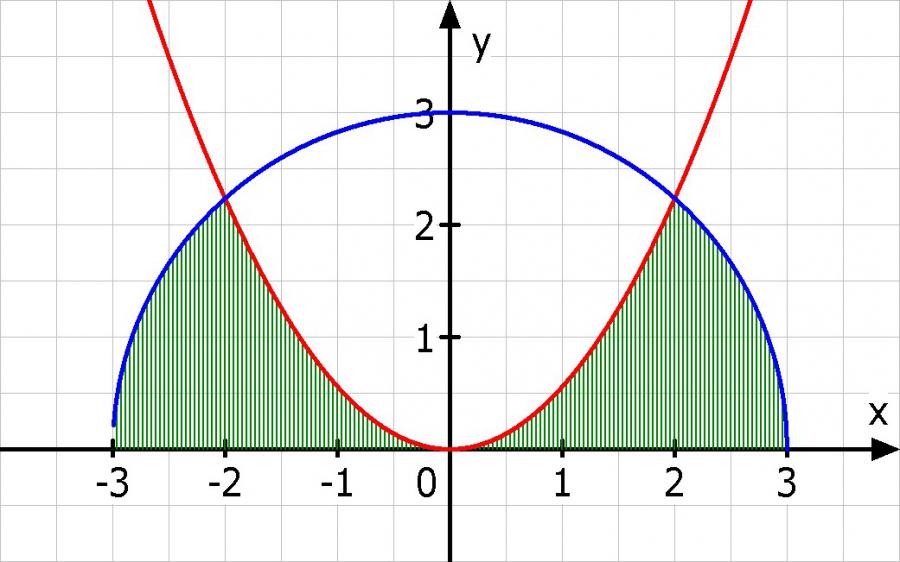
f(x) = a * x^2
g(x) = Wurzel(9 - x^2)
Zunächst müssen wir schauen wo g(x) die gerade y = Wurzel(5) schneidet. g(x) = Wurzel(5)
Wurzel(9 - x^2) = Wurzel(5)
Das ist sicher bei x = +- 2 der Fall.
Jetzt passen wir den Parameter a von f(x) so an das auch diese Funktion bei +- 2 der Wert von Wurzel(5) hat.
f(2) = a * 2^2 = Wurzel(5)
a = Wurzel(5) / 4
Damit haben wir die beiden Funktionen. Ich zeichne sie mal zur Unterstützung. Siehe unten. Wir sollten jetzt noch die Stammfunktionen bestimmen.
Die Fläche zu bestimmen ist jetzt recht einfach. Sie ergibt sich aus
2 * (F(2) - F(0) + G(3) - G(0))
Die Stammfunktionen finden wir mit
F(x) = Wurzel(5)/12 * x^3
G(x) = 9·asin(x/3)/2 + x*√(9 - x^2)/2
Damit ergibt sich die Fläche aus
A = 2 * (F(2) - F(0) + G(3) - G(0)) = (27·pi + 8·√5)/6 = 17.11859091
Die Fläche zwischen G und der x-Achse könnten wir aber auch über ein Kreisabschnitt berechnen. Ob man dabei direkt die Formel für den Kreisabschnitt nimmt oder vom Kreissegment ein Dreieck abzieht bleibt dabei jedem selbst überlassen. Je nachdem welche Formel man gerade im Kopf hat.