Quadratische Funktion fragen

Question

Ein Wasserstrahl wird parabelförmig durch einen Feuerwehrschlauch erzeugt. Dabei erreicht er eine Höhe von 20m und überwindet eine Distanz von 40m. Bestimme eine quadratische Funktion zur Modellierung des Wasserstrahls.

Answer 1

Drei Punkte A(0|0), S(20|20), B(40|0) auf der Parabel.

$$ f(x)=ax^2+bx+c $$

oder

$$ f(x)=a(x-x_S)^2+y_S$$

$$ f(x)=a(x-20)^2+20$$

$$ 0=a\cdot(0-20)^2+20 \Rightarrow a=-\frac{1}{20}=-0,05$$

$$ f(x)=-0.05\cdot(x-20)^2+20$$

Ausmultipliziert:

$$f(x)=-0.05x^{2}+2x$$

Answer 2

Ich würde dass jetzt so modellieren, dass der Strahl in (0/0) anfängt und in (40/0) aufhört. Am höchsten ist er in der Mitte, also ist der höchste Punkt bei (20/20).

Jetzt kennst du ja die allgemeine Form für quadratische Funktionen:

f(x) = a*\( x^{2} \)+b*x+c

Jetzt einfach die Bedingungen einsetzen:

1.)

 f(0) = 0 (Strahl fängt ja in (0/0) an)

a*0^2+b*0+c = 0

c=0

Da c=0 lasse ich es im folgenden einfach weg

2.) f(40)=0

a*40^2+b*40 = 0

a*1600 + b*40 = 0

3.) f(20) = 20

a*20^2 + b*20 = 20

a*400 + b*20 = 20

Mit 2 und 3 ergibt sich ein Lineares Gleichungssystem:

a*1600 + b*40 = 0

a*400 + b*20 = 20

was du mit deiner Lieblingsmethode lösen kannst. Ich nehme mal das Einsetzungsverfahren:

I) a*1600 + b*40 = 0  => a = -b/40

II) Einsetzen gibt (-b/40)*400+b*20 = 20 => b=2
III) Wieder in die erste Gleichung einsetzen a*1600+(2)*40 = 0 => a) - 1/20
Jetzt bist du fertig, denn a, b und c sind bestimmt, die Parabel ist 
f(x) = - 1/20 * x^2 + 2*x + 0 = - 1/20 * x^2 + 2*x 

Answer 3

Etwas kreativ und sehr einfach.

Wenn man mal den Ursprung des Koordinatensystems in den Scheitelpunkt des Wasserstrahls legt muss ein weiterer Punkt der Parabel P(40/2 | -20) oder P(20 | -20) sein.

Wenn wir also

y = a·x^2

mal nach a auflösen ergibt sich

a = y/x^2

Wir können hier also mal die x- und y-Koordinate von P einsetzen und a bestimmen.

a = -20/20^2 = -1/20 = -0.05

Die Parabel könnte also wie folgt aussehen.

y = -0.05·x^2

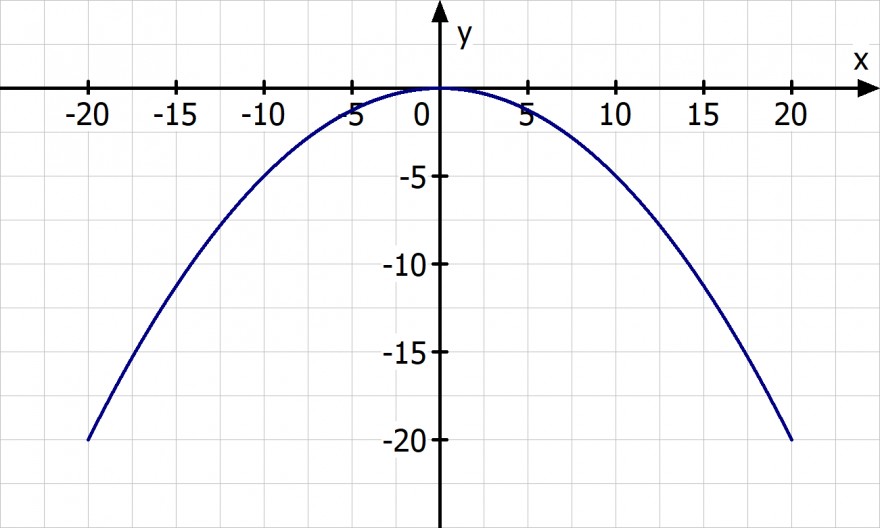
Wir können die Parabel aber auch um 20 Einheiten nach oben verschieben

y = -0.05·x^2 + 20

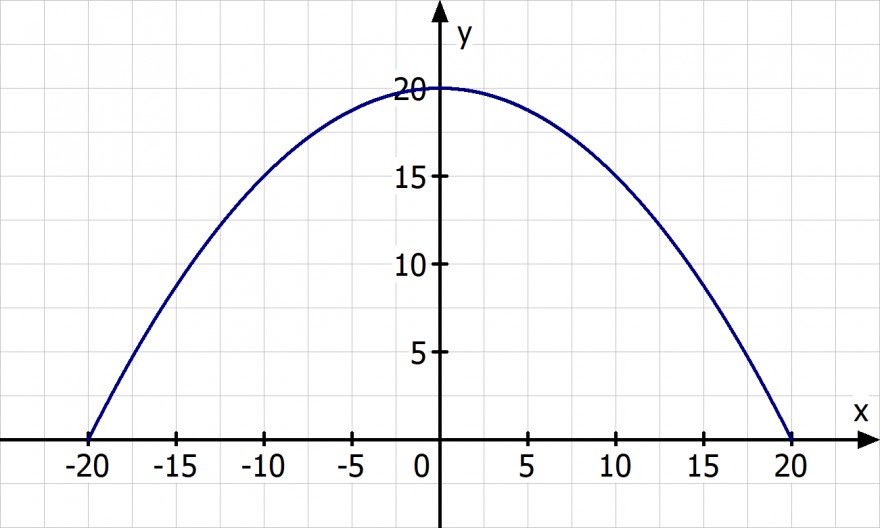
Oder noch zusätzlich um 20 Einheiten nach rechts verschieben.

y = -0.05·(x - 20)^2 + 20

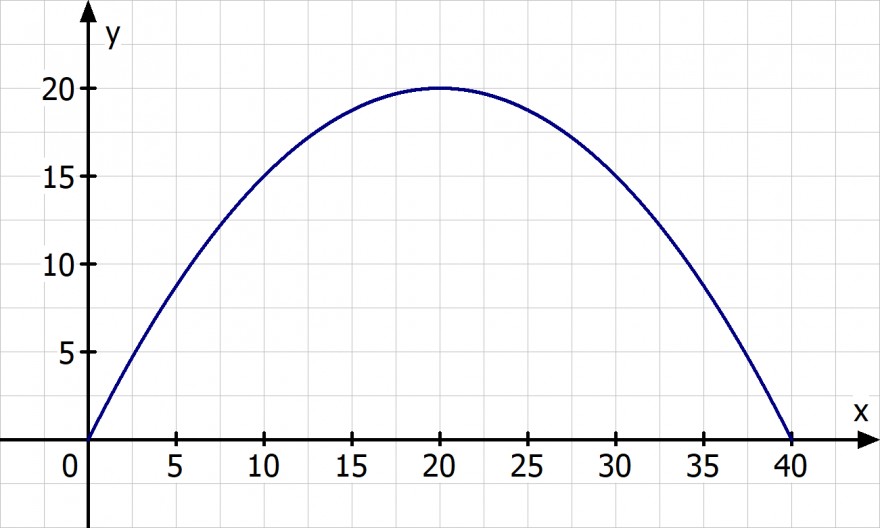
Der der Öffnungsfaktor überall gleich bleibt sollte man sich die Berechnung einprägen

a = Δy / (Δx)² = (Py - Sy) / (Px - Sx)²

Wobei P(Px | Py) ein beliebiger Punkt und S(Sx | Sy) der Scheitelpunkt der Parabel ist.

Da dir prinzipiell die Wahl des Koordinatensystems frei gestellt ist hättest du hier aber bereits nach der ersten Version aufhören können. Trotzdem sollte man wissen wie die anderen Versionen funktionieren, weil es durchaus üblich ist den Erdboden mit y = 0 zu beschreiben.

Aber du könntest jetzt auf dieser Grundlage auch super modellieren was passiert, wenn der Schlauch nicht auf dem Boden liegt und von dort den Wasserbogen erzeugt sondern wenn er in einer Höhe von 1.5 m gehalten wird und von dort diesen Bogen erzeugt. Die Möglichkeiten die man durch das Verschieben hat sind dabei sehr vielfältig.