Zeigen Sie, dass die Abbildung f linear ist und bestimmen Sie Mat(f)

Question

Zeigen Sie, dass die Abbildung f linear ist und bestimmen Sie Mat_B,B(f ) in den folgenden Fällen:
1. Betrachten Sie IR² mit B der kanonischen Basis, und sei f : IR² → R² die Drehung um 90° im mathematisch positiven Sinne.
2. Betrachten Sie IR² mit B der kanonischen Basis, und sei f : IR² → IR² die Spiegelung an der Geraden y = x.
3.Betrachten Sie Q(√2) als Q-Vektorraum mit der Basis B = (1,√2). Sei f : Q(√2) → Q(√2) die Multiplikation mit α + β
√2, also f (x) = x(α + β√2).

 

Wäre super, wenn sich jemand der Aufgaben annehmen könnte, da ich weniger als Bahnhof verstehe und Mathe schon kritisch wird so langsam. Über einen Lösungsweg wäre ich dankbar, damit ich es lernen und nachvollziehen kann.

Comments

kannst du noch mal 1-3 schritt für schritt aufschreiben also so, wie ich das aufschreiben muss ich komme gar nicht klar mit den ganzen schritten jetzt :-(

---

Eigentlich steht in der Lösung schon alles. Wenn du unbedingt mehr schreiben willst:

Schreib einfach 3. aus der Lösung und 1 und 2 aus dem Kommentar ab (inkl. Skizzen) und erklär mir, welchen Schritt du da nicht verstehst.

Ausführlicher geht das mit unserer Theorie gar nicht.

Answer 1

Bei 1 und 2 kannst du die Bildvektoren der Basisvektoren in die Spalten der Abbildungsmatrix setzen.

Durch die Angaben dieser Matrizen ist dann gezeigt, dass die Abbildung linear ist.

 

3.Betrachten Sie Q(√2) als Q-Vektorraum mit der Basis B = (1,√2). Sei f : Q(√2) → Q(√2) die Multiplikation mit α + β 
√2, also f (x) = x(α + β√2).

Nun machen wir dasselbe mit 3.

Das Bild von 1 ist f(1) = (α + β√2)

Das Bild von √2 ist f(√2) = √2(α + β√2) = α√2  +2 β = 2 β + α√2 

Ich gebe die Matrix an und rechne zur Probe (m + n√2) B₃

Ab hier mit A und B für Alpha und Beta nach Rechenregeln in Q

(m + n√2)(A + B√2) = mA + n√2 A + mB√2 + 2 nB = (mA + 2nB) + (mB + nA)√2

Das stimmt mit dem oben resultierenden Vektor überein.

Nochmals: Du musst i.d.R. nicht zeigen, dass einzelne lineare Abbildungen linear sind, wenn du die Matrizen hast und die nur Elemente aus dem verwendeten Körper enthalten.

 

 

Comments

Hi Lu,

könntest du die 1. vielleicht etwas ausführlicher erklären? Also damit auch die dummen das verstehen... :-)

1. Betrachten Sie IR2 mit B der kanonischen Basis,   (.....)

(hier habe ich schon den Faden verloren.... Was ist denn die kanonische Basis von R²?

Ich kann nicht nachvollziehen, wie du jetzt auf B1 und B2 kommst.

 

(......) und sei f : IR2 → R2 die Drehung um 90° im mathematisch positiven Sinne.

 

kann ich die Drehung so berechnen:

A * B = A'

A^-1 * A * B = A^-1 * A'

B = A^-1 * A'

A wäre (a b, c d) und A' wäre (c a, d b) Also um 90° gedreht.

---

Es wäre wohl schlauer, wenn das jemand beantworte würde, der den Zusammenhang aus eurem Kurs/Unterricht versteht.

Schon die Aufgabenstellung zeigt, dass wir wohl einen anderen Theorieaufbau haben. Man soll zuerst zeigen, dass die Abbildung linear ist und dann eine Matrix angeben. Aber Matrizen beschreiben ja lineare Abbildungen. Da erübrigt sich ein Beweis.

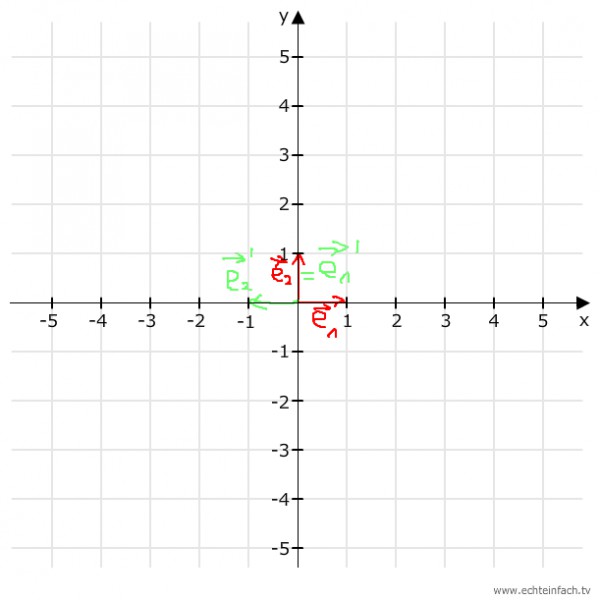
Ich beginne mal. IR^2 oder R x R ist das 'normale' xy-Koordinatensystem.

Die kanonische Basis dort die Vektoren e1= (1/0) und e2=(0/1)       [sollten Spaltenvektoren sein, zudem Pfeile auf e ergänzen]

Drehung um 90° geht im Gegenuhrzeigersinn um den Punkt (0/0), den sog. Koordinatenursprung.

Nun die Bildvektoren von e1 und e2

e1' zeigt in y-Richtung. Also e1' = (0/1)

e2' zeigt in neg. x-Richtun. Also e2' = (-1/0)

Und das sind jetzt die Spaltenvektoren der Abbildungsmatrix.

B₁ = (0 -1)

          1   0

Du kannst ein paar Punkte der Ebene als Spaltenvektoren einsetzen und B₁ mit diesen Spalten multiplizieren, dann siehst du, wie die jeweils um 90° um (0/0) drehen.

Bsp. mit dem allg. Punkt (a/b)

(0 -1)             ( a  )                ( 0*a -1*b    )                  (   -b     )

 1 0           *      b            =       1*a + 0*b               =          a

 

---

noch zu B₂

Spiegelung an x=y heisst an der Winkelhalbierenden im 1. Quadranten.

e1' zeigt in y- Richtung: e1' = (0/1)

e2' zeigt in x-Richtung: e2' = (1|0)

Das sind wieder die Spaltenvektoren der Abbildungsmatrix.

B₂ = ( 0   1)

            1    0

 

Probe

Ich nehme nochmals einen allg. Punkt P(a/b) und zeige, wie's funktioniert.

 

(0 1)             ( a  )                ( 0*a +1*b    )                  (   +b     )

 1 0           *      b            =       1*a + 0*b               =          a

Hier werden einfach die x- und die y-Koordinate der Punkte vertauscht. Das wollen wir, wenn wir an y=x spiegeln.

---

Nachtrag: Bei mir sind B₁, B₂ und B₃ Abbildungsmatrizen. Du benutzt dafür glaub ich A. B scheint bei dir Basis zu bedeuten. 

---

Kannst du bitte noch einmal 1-3 schritt für schritt aufschreiben, wie man es aufschreiben würde? Ich muss die Frage auch machen und ich komme gerade gar nicht klar mit den ganzen geschriebenen sachen und den skizzen :(