Ich habe die Aufgabe mal unter folgendem Link bearbeitet: https://docs.google.com/document/d/1mGvjW5sF6Gv7L04fP1u9oQ9IYxtq0WONaBvgdsLiWN8/pub
Kurvendiskussion: f(x) = x·(3 - √x)
Funktion und Ableitungen
f(x) = x·(3 - √x) = 3·x - x^{3/2}
f'(x) = 3 - 3/2·√x
f''(x) = - 3/(4·√x)
Definitionsbereich
D = R0+
Y-Achsenabschnitt f(0)
f(0) = 0
Nullstellen f(x) = 0
x·(3 - √x) = 0
x1 = 0
3 - √x = 0
√x = 3
x2 = 9
Verhalten an den Grenzen des Definitionsbereiches
f(0) = 0
lim (x → ∞) x·(3 - √x) = - ∞
Extremstellen f'(x) = 0 mit Monotonieverhalten
3 - 3/2·√x = 0
x = 4
f(4) = 4 [Hochpunkt]
Für x < 4 monoton steigend und für x > 4 monoton fallend.
Wendestellen f''(x) = 0 mit Krümmungsverhalten
- 3/(4·√x) = 0
Ein Bruch wird Null, wenn der Zähler Null wird. Das ist hier nie der Fall. Daher gibt es keine Wendestelle.
- 3/(4·√x) < 0
Damit ist die Funktion im ganzen Definitionsbereich rechtsgekrümmt.
Zusatzaufgaben
Berechnen der Funktionswerte f(3), f(6) und f(11)
f(3) = 9 - 3·√3 = 3.803847577
f(6) = 18 - 6·√6 = 3.303061543
f(11) = 33 - 11·√11 = -3.482872693
Tangentengleichungen in den Nullstellen
x0 = 0
f(x0) = f(0) = 0
f'(x0) = f'(0) = 3
t1(x) = f'(x0)·(x - x0) + f(x0) = 3·(x - 0) + 0 = 3·x
x0 = 9
f(x0) = f(9) = 0
f'(x0) = f'(9) = - 3/2
t2(x) = f'(x0)·(x - x0) + f(x0) = - 3/2·(x - 9) + 0 = 13.5 - 1.5·x
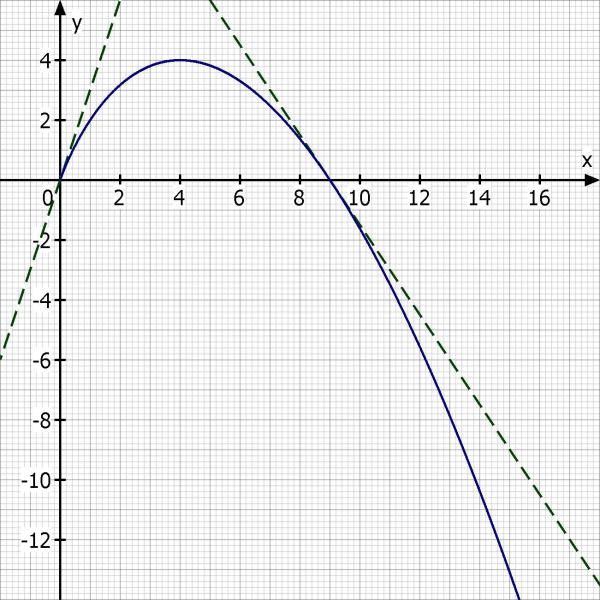
Skizze der Funktion mit Tangenten