Eine Konsumentenschutzorganisation untersucht das Abfüllgewicht von bestimmten Konserven. Das auf der Konserve angegebene Gewicht beträgt 1000g. Außerdem geht man davon aus, dass das Gewicht normalverteilt ist. Eine Stichprobe der Größe 16 ergibt ein durchschnittliches Gewicht der Konserven von 960g und eine empirische Varianz von 18825g2.
Geben Sie die Obergrenze des 90%-Konfidenzintervalls für das durchschnittliche Abfüllgewicht der Konserven an.
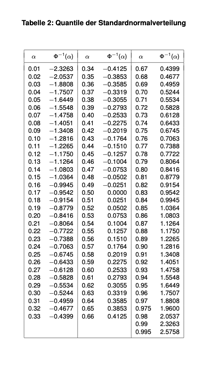
wie komme ich hier bei diesem Ergebnis auf den Faktor 1,7531?
Text erkannt:
Tabelle 21 Owentile der Stenderdneemalvertellung

Text erkannt:
$$ =[980-1.7531 \sqrt{\frac{18 \times 35}{16}} ; 960+1.7531 \sqrt{\frac{13 \times 25}{16}}] $$
[499.8668,1020.1332]
- Obergenet = 100013