Hallo Erdal,
wenn \(P\) an einer Ebene \(E\) gespiegelt zu \(P'\) wird, muss die Ebene genau zwischen diesen beiden Punkten liegen. Das bedeutet, dass der Punkt \(M\) $$M = \frac12 (P' + P ) = \begin{pmatrix}2\\ 1,5\\ 2,5\end{pmatrix}$$ein Punkt der Spiegelebene ist. So sähe das aus:
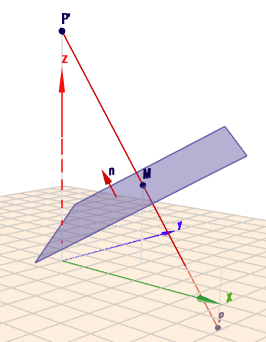
Und der Vektor zwischen \(P\) und \(P'\) muss senkrecht auf der Spiegelebene stehen. Damit kann man die Normalengleichung der Ebene bereits hinschreiben: $$\begin{aligned}E: \quad (P' - P) \vec x &= (P' - P) \cdot M \\ \begin{pmatrix}-4\\ -3\\ 9\end{pmatrix} \vec x &= \begin{pmatrix}-4\\ -3\\ 9\end{pmatrix} \cdot \begin{pmatrix}2\\ 1,5\\ 2,5\end{pmatrix} = 10 \end{aligned}$$Eine Koordinatengleichung der Ebene \(E\) lautet also $$E: \quad -4x - 3y + 9 z = 10$$