Globales Minimum und Maximum berechnen

Question

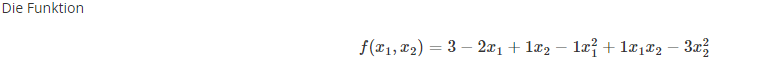
Text erkannt:

Die Funktion
$$f\left(x_{1}, x_{2}\right)=3-2 x_{1}+1 x_{2}-1 x_{1}^{2}+1 x_{1} x_{2}-3 x_{2}^{2}$$

besitzt genau einen stationären Punkt (x1,x2). Bestimmen Sie diesen. Welche der folgenden Aussagen treffen zu?


a. In (x1,x2) liegt ein globales Minimum vor.


b. In (x1,x2) liegt ein globales Maximum vor.


c. Es gilt x2=−1.


d. Es gilt x1=x2.


e. Es gilt x1=0.

Answer 1

f_x= -2-2x+y = 0 ==>   y = 2+2x

f_y= 1 + x - 6y = 0 einsetzen  1+x-6(2+2x) = 0

                                             1 + x - 12 - 12x = 0

                                                       -11x = 11 ==>   x = -1

Comments

Vielen Dank. Also ist ( x1,x2) = (-1,0)

Aber welche der Antwortmöglichkeiten sind dann richtig? c, d und e sind falsch oder? was ist mit a und b?

---

Die Hessematrix an der Stelle ist

-2    1
 1    -6

ist negativdefinit , also b) richtig .

Sagt Wolfram auch:

https://www.wolframalpha.com/input/?i=optimize+3-2x%2By-x%5E2%2Bxy-3…