Vom Duplikat:
Titel: Wie kommt man auf diese Lösungen?
Stichworte: gleichungen
Eine Folge ist definiert als an= (n2+1)/(n-1)-(n2+3n-2)/(n+1)
Berechnen Sie lim an n-> ∞
Ich habe das ganze nun mit dem Lösungsweg vergleichen aber verstehe nicht wie man auf die orange makierten Ergebnisse kommt..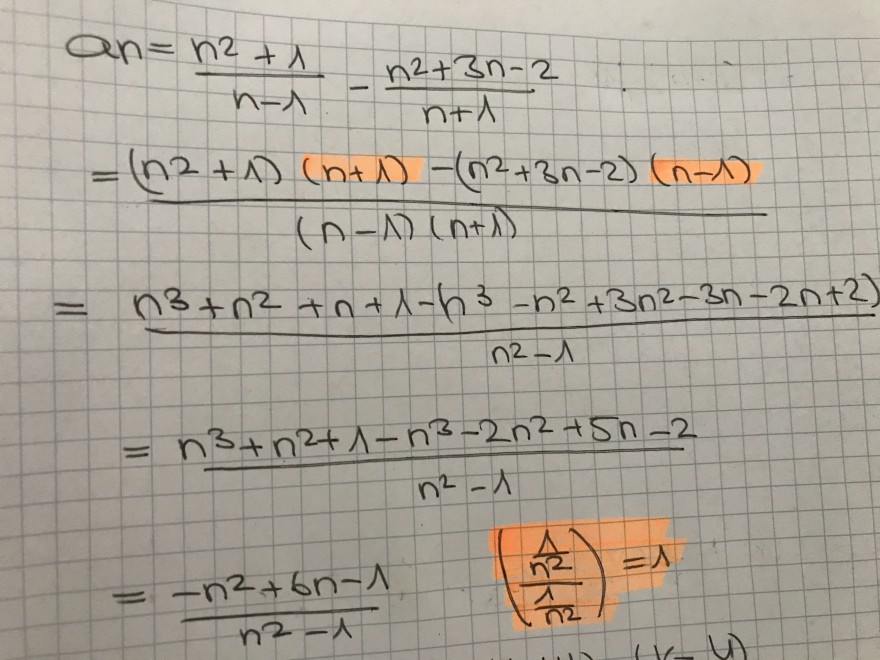
Text erkannt:
\( \begin{array}{l}\text { On }=\frac{n^{2}+1}{n-1}-\frac{n^{2}+3 n-2}{n+1} \\ =\frac{\left(n^{2}+1\right)(n+1)-\left(n^{2}+3 n-2\right)(n-1)}{(n-1)(n+1)} \\ = \\ \frac{n^{3}+n^{2}+n+1-n^{3}-n^{2}+3 n^{2}-3 n-2 n+2}{n^{2}-1} \\ =\frac{n^{3}+n^{2}+1-n^{3}-2 n^{2}+5 n-2}{n^{2}-1} \\ =\frac{-n^{2}+6 n-1}{n^{2}-1} & \left(\frac{n^{2}}{n^{2}}\right)=1\end{array} \)