Extremwertaufgabe bei Strecken: Welche Stelle am Bach muss angepeilt werden, damit der Weg möglichst kurz ist?

Question

Aufgabe:

Bei einem Wettbewerb Iäuft jede Starterin vom Start zum Ziel. Dazwischen muss sie von einem Bach Wasser in eine Flasche füllen. Entnimm die Entfernungen der Zeichnung. Welche Stelle am Bach muss angepeilt werden, damit der Weg möglichst kurz ist? Skizziere den Graphen der Zielfunktion im Intervall von 0 bis 160 und zeichne die Stelle der gesuchten Lösung ein. Wie groß sind die Extrema am Rand des Intervalls?

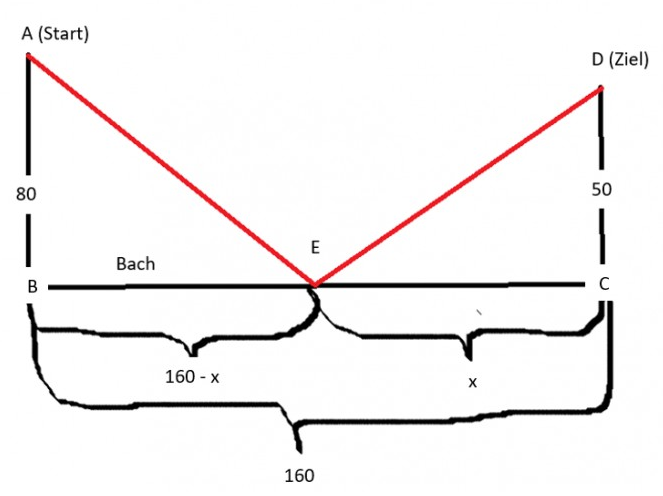
Problem/Ansatz:

Ich bin darauf gekommen, dass man es nur mittels Satz des Pythagoras lösen kann, doch ich schaffe es nicht, die Zielfunktion aufzustellen.

Answer 1

Das geht ganz ohne Analysis:

\( \frac{160-x}{80} \) =\( \frac{x}{50} \) nach x auflösen.

Answer 2

Zielfunktion: Länge der zu laufenden Strecke AE + ED

L(x) = √(  80^2 + (160-x)^2 )  +  √(  50^2 + x^2 )

Answer 3

Für die gesuchte Stelle gilt

50 - (50 + 80)/160·x = 0 --> x = 61.53846153

Skizze der Zielfunktion

~plot~ sqrt(80^2+(160-x)^2)+sqrt(50^2+x^2);x=61.54;[[0|160|0|300]] ~plot~

Answer 4

li ^2 = x^2 + 50^2
re ^2 = ( 160 - x ) ^2 + 80 ^2

G = gesamte Länge
G = √ ( x^2 + 50^2) + √ (( 160 - x ) ^2 + 80 ^2 )
G ´( x ) = 0

x = 800 / 13

Die Aufgabe wurde mit Hilfe eines Matheprogramms
gelöst. Dürft ihr bei dieser Aufgabe auch ein Programm
/ GTR butzen ?