Text erkannt:
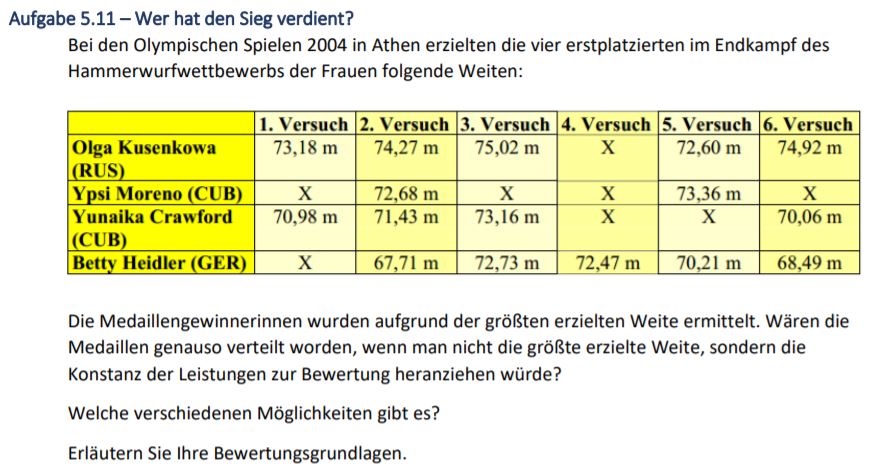
Aufgabe \( 5.11- \) Wer hat den Sieg verdient? Bei den Olympischen Spielen 2004 in Athen erzielten die vier erstplatzierten im Endkampf des
Hammerwurfwettbewerbs der Frauen folgende Weiten:
\begin{tabular}{|l|c|c|c|c|c|c|}
\hline & 1. Versuch & 2. Versuch & 3. Versuch & 4. Versuch & 5. Versuch & 6. Versuch \\
\hline Olga Kusenkowa (RUS) & \( 73,18 \mathrm{m} \) & \( 74,27 \mathrm{m} \) & \( 75,02 \mathrm{m} \) & \( \mathrm{X} \) & \( 72,60 \mathrm{m} \) & \( 74,92 \mathrm{m} \) \\
\hline Ypsi Moreno (CUB) & \( \mathrm{X} \) & \( 72,68 \mathrm{m} \) & \( \mathrm{X} \) & \( \mathrm{X} \) & \( 73,36 \mathrm{m} \) & \( \mathrm{X} \) \\
\hline Yunaika Crawford (CUB) & \( 70,98 \mathrm{m} \) & \( 71,43 \mathrm{m} \) & \( 73,16 \mathrm{m} \) & \( \mathrm{X} \) & \( \mathrm{X} \) & \( 70,06 \mathrm{m} \) \\
\hline Betty Heidler (GER) & \( \mathrm{X} \) & \( 67,71 \mathrm{m} \) & \( 72,73 \mathrm{m} \) & \( 72,47 \mathrm{m} \) & \( 70,21 \mathrm{m} \) & \( 68,49 \mathrm{m} \) \\
\hline
\end{tabular}
Die Medaillengewinnerinnen wurden aufgrund der größten erzielten Weite ermittelt. Wären die Medaillen genauso verteilt worden, wenn man nicht die größte erzielte Weite, sondern die Konstanz der Leistungen zur Bewertung heranziehen würde?
Welche verschiedenen Möglichkeiten gibt es?
Erläutern Sie Ihre Bewertungsgrundlagen.
Ich verstehe hier die Aufgabe nicht. Ich soll die Verteilung nach Konstanz der Leistungen aufstellen aber was genau heißt das ?