Aufgabe: Gegeben ist ein Würfel mit der Kantenlänge 5 in einem kartesischem Koordinatensystem
a) jede Seitenfläche des Würfels liegt in einer ebene. Geben Sie für jede dieser Ebenen eine Parameterdarstellung an.
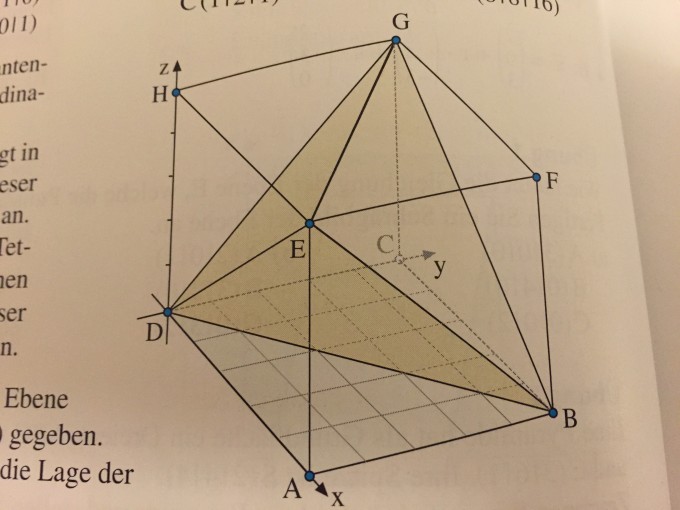
b) die Ecken D B G E bilden ein Tetraeder, dessen Seitendreiecke Ebenen aufspannen. Geben Sie für jede dieser Ebenen eine Parameter Darstellung an
Ich hab die Punkte abgelesen, aber bin mir unsicher: D (0/0/0) A (5/0/0) B (5/5/0) C (0/5/0) usw.
Ich weiß aber nicht wie ich für ein Rechteck oder Tetraeder eine Parameterdarstellung aufstelle. Ich weiß nur , wie es mit Dreiecken geht.
Mit Erklärung wäre nett, nur mit der Lösung kann ich nicht so viel anfangen
Text erkannt:
18