Hallo Emma,
Es ist ein Punkt \(Q\) gesucht, dessen Abstand zu \(P\) möglichst klein ist - also:
$$\begin{aligned} |Q-P| &\to \min \\ \implies F(Q) &= (Q-P)^2 \to \min \end{aligned}$$Die Nebenbedingung ist \(2x + 4y − z = 0\), somit ist die Lagrange-Funktion nebst Ableitungen usw.:
$$\begin{aligned} L(Q,\lambda) &= (Q-P)^2 + \lambda(2x + 4y − z = 0) \\ \frac{\partial L}{\partial Q} &= 2\left(Q-P \right) + \lambda \begin{pmatrix} 2\\4\\ -1 \end{pmatrix} = \vec 0 \\ \implies Q &= -\frac 12 \lambda \begin{pmatrix} 2\\4\\ -1 \end{pmatrix} + P \\ \end{aligned}$$
und heraus kommt eine Geradengleichung (substituiere \(- \frac 12 \lambda = t\)), die ich in die Nebenbedingung einsetze:
$$\begin{aligned} Q \begin{pmatrix} 2\\4\\ -1 \end{pmatrix} &= 0 \\ \left( \begin{pmatrix} 2\\4\\ -1 \end{pmatrix}t + P\right) \begin{pmatrix} 2\\4\\ -1 \end{pmatrix} &= 0 \\ (2^2 + 4^2 + (-1)^2) t + (2 + 0 \cdot 4 + (-1)) &= 0 \\ 21 t + 1 &= 0 \\ \implies t &= - \frac 1{21} \end{aligned}$$
setzt man das gefundene \(t\) in die Geradengleichung ein, so erhält man den gesuchten Punkt \(Q\)
$$Q = - \frac 1{21} \begin{pmatrix} 2\\4\\ -1 \end{pmatrix} + \begin{pmatrix} 1\\0\\ 1 \end{pmatrix} = \frac 1{21} \begin{pmatrix} 19\\-4\\ 22 \end{pmatrix} \approx \begin{pmatrix}0.905\\ -0.190\\ 1.048\end{pmatrix}$$
wenn man das ganze räumlich interpretiert, dann sieht es so aus:
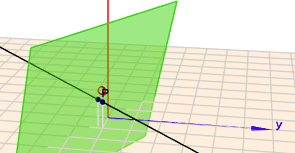
(klick auf das Bild, dann öffnet sich die Szene in 3D)
Die grüne Ebene zeigt die Nebenbedingung an und die schwarze Gerade ist das Ergebnis des Lagrange-Multiplikators. Der Schnittpunkt von beiden ist \(Q\). \(Q\) ist der Punkt der Ebene, der \(P\) am nächsten liegt.
zu b) Die Funktion und die Nebenbedingung sind $$ f(x,y) = 4y - x \to \text{opt.} \\ \text{NB.:} ~ 0 = x^{2} - xy + y^{2} - x + y - 4 $$
Damit lässt sich die Lagrange-Funktion aufstellen$$L(x,y,\lambda) = 4y - x + \lambda(x^{2} - xy + y^{2} - x + y - 4) $$Ableiten nach \(x\) und \(y\), Nullsetzen und das \(\lambda\) eliminieren gibt$$\begin{aligned}\frac{\partial L}{\partial x} &= -1 + \lambda(2x-y-1) = 0 \\ \frac{\partial L}{\partial y} &= 4 + \lambda(-x + 2y + 1) = 0 \\ -4(2x-y-1) &= -x + 2y + 1 \\ -8x + 4y + 4 &= -x + 2y + 1 \\ 3 &= 7x - 2y \\ y &= \frac 12 (7x-3) \end{aligned}$$Und wenn man dies in die Nebenbedingung einsetzt, so bleibt eine quadratische Gleichung mit den Lösungen\(x_1 = 1\) und \(x_2=-1/3\). Graphisch sieht das so aus:
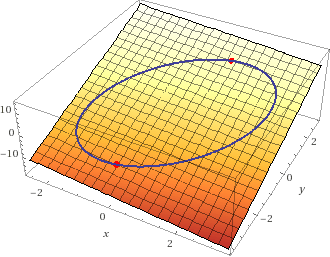
Das ist eine Ellipse (die Nebenbedingung), die in einer (schiefen) Ebene liegt. Das Maximum auf dieser Ellipse liegt bei$$(x,y)_{\max} = \begin{pmatrix} 1& 2\end{pmatrix}, \quad f(1,2) = 7$$und das Minimum liegt bei$$(x,y)_{\min} = \begin{pmatrix} -\frac 13& -\frac 83\end{pmatrix}, \quad f\left( -\frac 13, -\frac 83\right) = -\frac {31}3$$