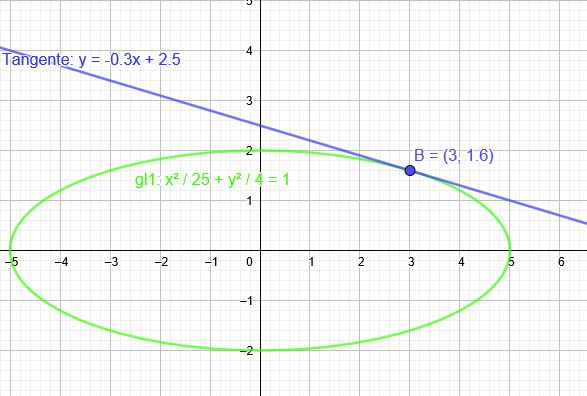
Halbachsenlängen a und b dieser Ellipse herausfinden ell: \(\frac{x^2}{a^2} + \frac{y^2}{b^2}=1\)
Die Gerade berührt die Ellipse im Punkt \(B(\red{3}|\blue{1,6})\)
Gerade t: \(y= -0,3x + 2,5\) \(m=-0,3\)
\(\frac{x^2}{a^2} + \frac{y^2}{b^2}=1\)
\(f(x,y)=b^2x^2+a^2y^2-1\)
\(f_x(x,y)=2b^2x\) \(f_x=6b^2\)
\(f_y(x,y)=2a^2y\) \(f_y=3,2a^2\)
\(f´(3)=- \frac{6b^2}{3,2a^2} \)
\(-0,3=- \frac{6b^2}{3,2a^2} \) \(0,3= \frac{6b^2}{3,2a^2} \) \(b^2=0,16a^2\)
\(B(\red{3}|\blue{1,6})\) liegt auf \(\frac{x^2}{a^2} + \frac{y^2}{b^2}=1\) → \(\frac{9}{a^2} + \frac{2,56}{0,16a^2}=1\)
\(a^2=25\) \(b^2=4\)
Halbachsenlängen: \(a=5\) \(b=2\)
Ellipse: \(\frac{x^2}{25} + \frac{y^2}{4}=1\)