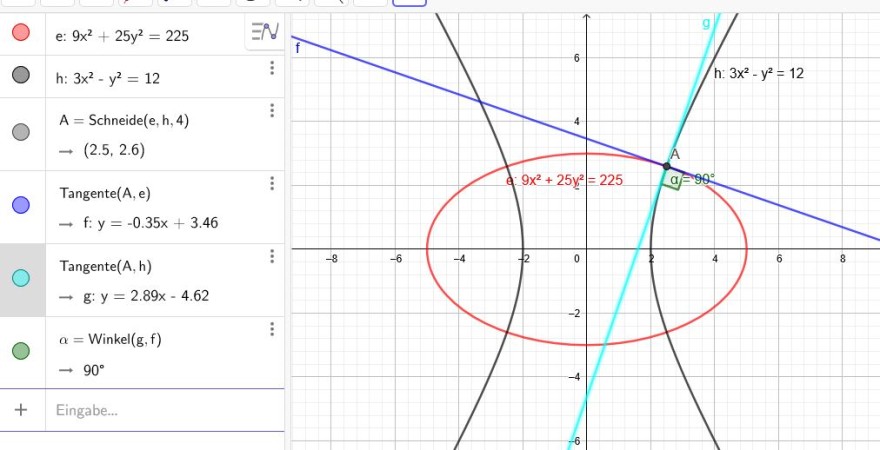
Ellipse : \(9x^2 +25y^2=225\) Hyperbel: \(3x^2-y^2 =12\)
Berechnen Sie die Schnittpunkte und den Schnittwinkel der Ellipse und der Hyperbel.
\(y^2=3x^2-12\) in \(9x^2 +25y^2=225\) einsetzen:
\(9x^2 +25\cdot(3x^2-12)=225\)
\(x_1=2,5\) \(y^2=3\cdot 2,5^2-12=6,75\) \(y_1=\sqrt{6,75}\)
Die weiteren Schnittpunkte werden nicht benötigt.
Tangentengleichung an die Ellipse:
\(9x^2 +25y^2=225\) im Punkt B\((2,5|\sqrt{6,75})\)
\(9x\cdot 2,5 +25y\cdot \sqrt{6,75} =225\) \(y\cdot \sqrt{6,75} =9-0,9x \)
\(y =-\frac{0,9}{\sqrt{6,75}}x+\frac{9}{\sqrt{6,75}} \) \(m_1=-\frac{0,9}{\sqrt{6,75}}\)
Tangentengleichung an die Hyperbel:
\(3x\cdot 2,5-y \cdot \sqrt{6,75}=12\) \( y \cdot \sqrt{6,75}=7,5x-12\)
\( y =\frac{7,5}{\sqrt{6,75}}x-\frac{12}{\sqrt{6,75}}\) \(m_2=\frac{7,5}{\sqrt{6,75}}\)
\(\tan(α)=|\frac{m_2-m_1}{1+m_1m_2}| \)
\(\tan(α)=|\frac{\frac{7,5}{\sqrt{6,75}}+\frac{0,9}{\sqrt{6,75}}}{1-\frac{0,9}{\sqrt{6,75}}\cdot \frac{7,5}{\sqrt{6,75}}}| \)
\(\tan(α)=|\frac{a}{b} | \)Hier wird der Nenner 0, somit ist \(α=90° \)
Oder \(m_1\cdot m_2= -\frac{0,9}{\sqrt{6,75}} \cdot \frac{7,5}{\sqrt{6,75}}=-\frac{6,75}{6,75}=-1\)