Ellipse und Hyperbel ....

Question

Aufgabe:

Ellipse : 9x² +25y²=225

Hyperbel: 3x²-y² =12

Problem/Ansatz:

Berechnen Sie die Schnittpunkte  und den Schnittwinkel der Ellipse und der Hyperbel

Vielen Dank im Voraus !!!!

Answer 1

Die Schnittpunkte :

Answer 2

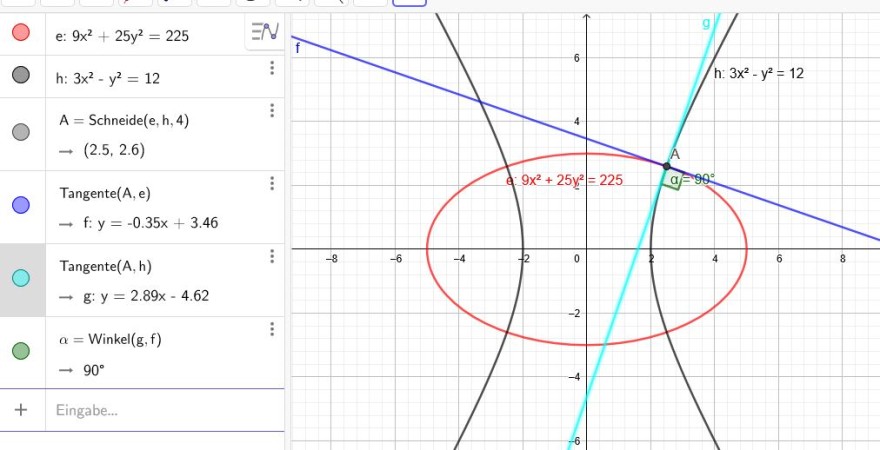
Ellipse : $9x^2 +25y^2=225$     Hyperbel: $3x^2-y^2 =12$

Berechnen Sie die Schnittpunkte und den Schnittwinkel der Ellipse und der Hyperbel.

$y^2=3x^2-12$  in   $9x^2 +25y^2=225$ einsetzen:

$9x^2 +25\cdot(3x^2-12)=225$

 $x_1=2,5$       $y^2=3\cdot 2,5^2-12=6,75$      $y_1=\sqrt{6,75}$

Die weiteren Schnittpunkte werden nicht benötigt.

Tangentengleichung an die Ellipse:

$9x^2 +25y^2=225$ im Punkt B$(2,5|\sqrt{6,75})$

$9x\cdot 2,5 +25y\cdot \sqrt{6,75} =225$           $y\cdot \sqrt{6,75} =9-0,9x$

$y =-\frac{0,9}{\sqrt{6,75}}x+\frac{9}{\sqrt{6,75}}$    $m_1=-\frac{0,9}{\sqrt{6,75}}$

Tangentengleichung an die Hyperbel:

$3x\cdot 2,5-y \cdot \sqrt{6,75}=12$          $y \cdot \sqrt{6,75}=7,5x-12$

$y =\frac{7,5}{\sqrt{6,75}}x-\frac{12}{\sqrt{6,75}}$     $m_2=\frac{7,5}{\sqrt{6,75}}$

$\tan(α)=|\frac{m_2-m_1}{1+m_1m_2}|$

$\tan(α)=|\frac{\frac{7,5}{\sqrt{6,75}}+\frac{0,9}{\sqrt{6,75}}}{1-\frac{0,9}{\sqrt{6,75}}\cdot \frac{7,5}{\sqrt{6,75}}}|$

$\tan(α)=|\frac{a}{b} |$Hier wird der Nenner 0, somit ist $α=90°$

Oder $m_1\cdot m_2= -\frac{0,9}{\sqrt{6,75}} \cdot \frac{7,5}{\sqrt{6,75}}=-\frac{6,75}{6,75}=-1$

Comments

Du bist ja richtig lernfähig.

(Abgesehen von dem Lapsus:)

Die weiteren Schnittpunkte werden nicht benötigt.

---

Die weiteren Schnittpunkte werden nicht benötigt.

Vielleicht, weil die ja bereits vollständig richtig von Grosserloewe angegeben worden waren.
Dann braucht man sich damit ja nicht aufhalten.

---

Andere vernünftige Antworten haben ihn doch noch nie gestört.