Berechnen Sie die Koordinaten der Bilder der Punkte POI(xm+40 l α.

Question

\( \vec{a} \) Aufgabe:

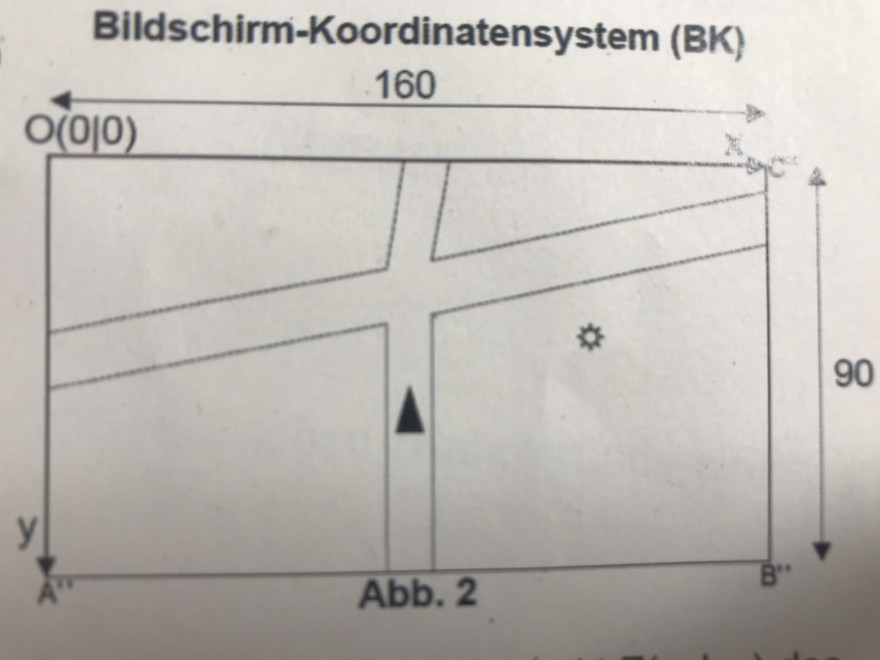
Bei der Programmierung von Navigationssystemen muss die im Karten-Koordinatensystem (Abb.1) dargestellte digitalisierte Karte, auf das Display des Navigationssystems (Abb.2) abgebildet werden.

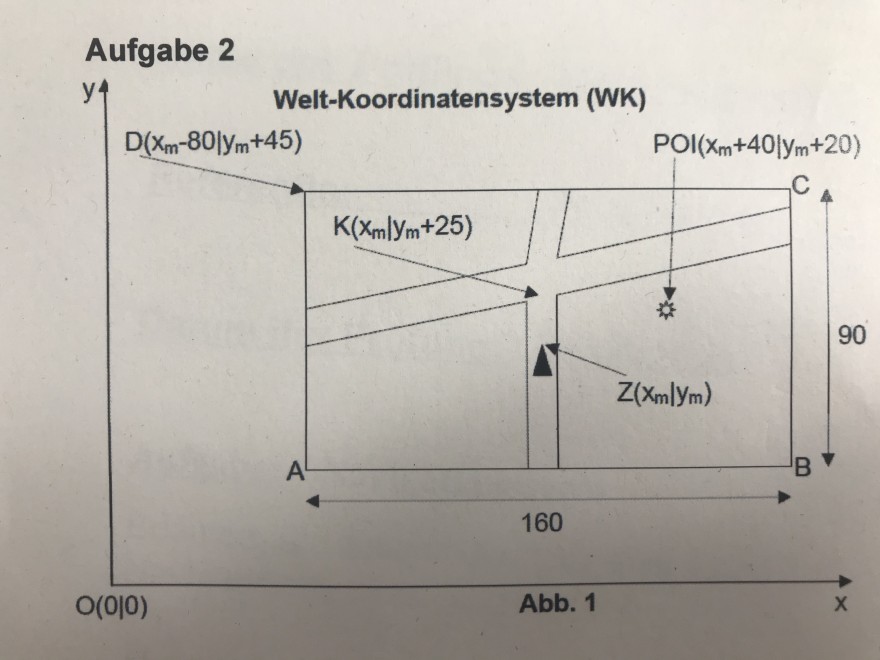
Dieser Vorgang kann vereinfacht folgendermaßen beschrieben werden: Mit Hilfe des Global - Positionen Systems, kurz GPS, wird ermittelt, in welchem Punkt Z( Xm l Ym ) des Welt-Koordinatensystems (WK) sich z.B. ein Fahrzeug befindet. Dieser Punkt ist Zentrum eines rechteckigen Kartenausschnitts (Rechteck ABCD), der dieselben Maße wie das Bildschirm-Koordinatensystem (BK) besitzt (160x90 Pixel).

Der rechteckige Kartenausschnitt im WK wird nun mit Hilfe einer affinen Abbildung auf das BK abgebildet, d.h. jeder Punkt oder genauer jeder Ortsvektor \( \vec{x} \) eines Punktes des Kartenausschnittes wird eindeutig auf einen Ortsvektor \( \vec{x} \) ' eines Punktes des BK abgebildet. Im BK ist, wie bei Computergraphiken üblich, die y-Achse nach unten positiv orientiert.

1.1 Erläutern sie den Vorgang, in dem Sie z.B. den Punkt Z(558020l5931836) betrachten.

1.1.1 Bestimmen sie die Koordinaten der Eckpunkte A, B, C, und D des rechteckigen Kartenausschnitts im Welt-Koordinatensystem.

1.1.2 Bestimmen sie die Bilder Z', A', B', C' und D' der Punkte Z, A, B, C und D für die Abbildung

α₁ : \( \begin{pmatrix} x°\\y° \end{pmatrix} \) = \( \begin{pmatrix} x\\y \end{pmatrix} \) \( \begin{pmatrix} Xm−80\\Ym+45 \end{pmatrix} \)

1.1.3 Bestimmen sie die Bilder Z'', A'', B'', C'', und D'' der Punkte Z', A', B', C' und D' für die Abbildung

α₂ : \( \begin{pmatrix} x'\\y' \end{pmatrix} \) = \( \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \) ×\( \begin{pmatrix} x°\\y° \end{pmatrix} \)

1.2 Begründen Sie, dass die Umrechnung der Punkte des WK in das BK durch folgende affine Abbildung beschrieben werden kann:  α: \( \begin{pmatrix} x'\\y' \end{pmatrix} \) = \( \begin{pmatrix} 1 & 0 \\ 0 & −1 \end{pmatrix} \) × ( \( \begin{pmatrix} x\\y \end{pmatrix} \) − \( \begin{pmatrix} Xm−80\\Ym+45 \end{pmatrix} \) )

Berechnen Sie die Koordinaten der Bilder der Punkte POI(xm+40 l ym+20) (Point of Interest) und K(xm l ym+25) (Kreuzung) für die Abbildung α.

1.3 Unterschreitet ein Fahrzeug eine gewisse Geschwindigkeit oder soll ein Abbiegevorgang stattfinden, so wird der Kartenausschnitt im BK mit dem Faktor λ > 1, λ ∈IR vergrößert. Fixpunkt ist hierbei der Mittelpunkt des BK.

1.3.1 Bestimmen Sie die affine Abbildung β, die jedem Ortsvektor \( \vec{x} \) ' eines Punktes des BL den Ortsvektor \( \vec{x} \) '' des Bildpunktes nach der Vergrößerung zuordnet.

1.3.2 Prüfen Sie, ob sich für λ = 1,5 die Bilder der Punkte POI und K im sichtbaren Bereich des BK befinden.

Problem/Ansatz:

Text erkannt:

Bildschirm-Koordinatensystem (BK) 160
\( 0(0 | 0) \)
\begin{tabular}{|c|c|}
\hline & \\
\hline & \\
\hline & \\
\hline
\end{tabular}

 

Text erkannt:

Aufgabe 2
y \( \quad \) Welt-Koordinatensystem (WK)
A 1
\( \mathrm{O}(0 | 0) \)
bb.