Aufgabe:
Aus einem zylinderförmigen Baumstamm wurde für eine moderne Parkbank ein keilförniger Teil herausgeschnitten. Berechne den Oberflächeninhalt und das Volumen der Parkbank.
Problem/Ansatz:
Meine Rechnung lautet folgendes, ist sie richtig?:
Ausschnitt: alpha/360° = 260° /360° ≈ 0,72
Berechnung:
G = π * r² = π * (40 cm)² - 0,72 * (π * (40 cm)² ) ≈ 1407,4 cm²
M = 2π * r * h = 2π * 40 cm * 80 cm – 0,72 * (2π * 40 cm * 80 cm) ≈ 5629,7 cm²
O = 2 * G + M = 2 * 1407,4 cm² + 5629,7 cm² ≈ 8444,5 cm²
V = π * r² * h – Auschnitt = π * (40 cm)² * 80 cm – 0,72 * (π * (40 cm)² * 80 cm) ≈ 112594,7 cm³
Antwort: Der Oberflächeninhalt beträgt 8444,5 cm², das Volumen hierbei 112594,7 cm³.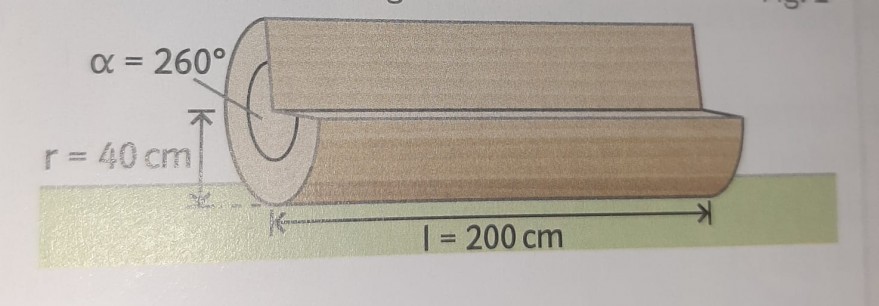
Text erkannt:
\( \alpha=260^{\circ} \)
\( r=40 \mathrm{cm}^{\pi} \)
\( |=200 \mathrm{cm} \)