f(x) = a·x^4 + b·x^3 + c·x^2 + d·x + e
f'(x) = 4·a·x^3 + 3·b·x^2 + 2·c·x + d
f''(x) = 12·a·x^2 + 6·b·x + 2·c
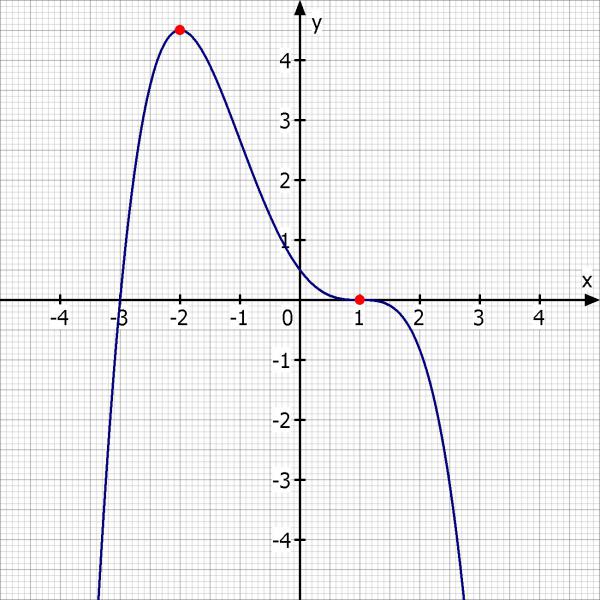
Der Sattelpunkt des Graphen einer ganzrationalen Funktion 4.Gerades ist S(1/0), der Hochpunkt (-2/4,5)
f(1) = 0
a + b + c + d + e = 0
f'(1) = 0
4·a + 3·b + 2·c + d = 0
f''(1) = 0
12·a + 6·b + 2·c = 0
f(-2) = 4.5
16·a - 8·b + 4·c - 2·d + e = 9/2
f'(-2) = 0
- 32·a + 12·b - 4·c + d = 0
Kontrolllösung: a = - 1/6 ∧ b = 0 ∧ c = 1 ∧ d = - 4/3 ∧ e = 1/2
Funktion: f(x) = - 1/6·x^4 + x^2 - 4/3·x + 1/2
Skizze: