Kurven und Vektorfeld skizzieren

Question

Es sei diese Kurve gegeben:
$$ \gamma:[0, \pi] \rightarrow \mathbb{R}^{2}, t \mapsto\left(\begin{array}{c} t^{2} \sin t \\ t^{2} \cos t \end{array}\right) $$
a) Berechnen Sie das Kurvenintegral \( \int \limits_{\gamma} x d x+y d y \)
$$ \begin{aligned} x=t^{2} \sin t & \Rightarrow d x=2 t \sin t+t^{2} \cos t \\ y &=t^{2} \cos t \Rightarrow d y=2 t \cos t-t^{2} \sin t \\ \int x d x+y d y &=\int \limits_{0}^{2} t^{2} \sin t \cdot\left(2 t \sin t+t^{2} \cos t\right)+t^{2} \cos t \cdot\left(2 t \cos t-t^{2} \sin t\right) d t \\ &=\int \limits_{0}^{2} 2 t^{3} \sin ^{2} t+t^{4} \sin t \cos t+2 t^{3} \cos ^{2} t-t^{4} \cos t \sin t d t \\ &=\int \limits_{0}^{\pi} 2 t^{3} d t=\left[\frac{2}{4} t^{4}\right]_{0}^{\pi}=\frac{2}{4} \pi^{4}-\frac{2}{4} \cdot 0^{4}=\frac{\pi^{4}}{2} \end{aligned} $$
b) Skizzieren Sie die Kurve und das zum Kurvenintegral gehörige Vektorfeld.

Ich komme hier nicht weiter. Wie soll ich die Kurve  und das Vektorfeld skizieren?

Kann man das auch mit Hilfe eines Programms lösen?

Liebe Grüße

Answer 1

Hallo

 die Kurve ist eine Spirale, die du auch selbst skizzieren kannst. ohne das t^2 ist es ein Kreis, mit t^2 ist es eine Spirale , da der Radius mit t^2 wächst . also bei pi schon größer 9 ist bei 2pi ca 39.

Ich lass so was von geogebra plotten, ein freies Programm was oft hilft. hier das Beispiel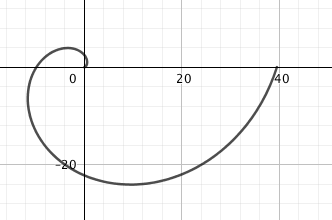

das Vektorfeld ist wohl einfach (x,y) also zeichne kurze Pfeilchen mit der Richtung (x,y) an die entsprechendem Stellen, auf der Winkelhalberenden y=x Pfeile mit Steigung 1, , beim Punkt (2,1) mit Steigung 1/2 usw.

Gruss lul